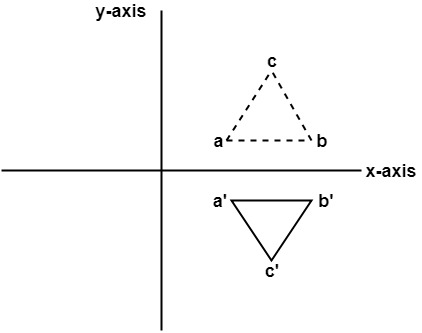
Reflect across y=2x Natural Language; 1 Reflection Over The XAxis Sets of Coordinates If you have a set of coordinates, place a negative sign in front of the value of each yvalue, but leave the yvalue the same Example question #1 Reflect the following set of coordinates over the xaxis (4, 6), (2, 4), (0, 0), (2, 4), (4, 6) Solution Step 1 Place a negative sign in front of each ycoordinateLine of symmetry using a reflection matrix For a reflection over the xaxis yaxis line y = x Multiply the vertex matrix on the left by Reflection Matrices Example 4 Find the coordinates of the image of pentagon PENTA with P(4 ,3), E(1, 4), N(1, 3), T(0, 1), and A(3, 1) after a reflection
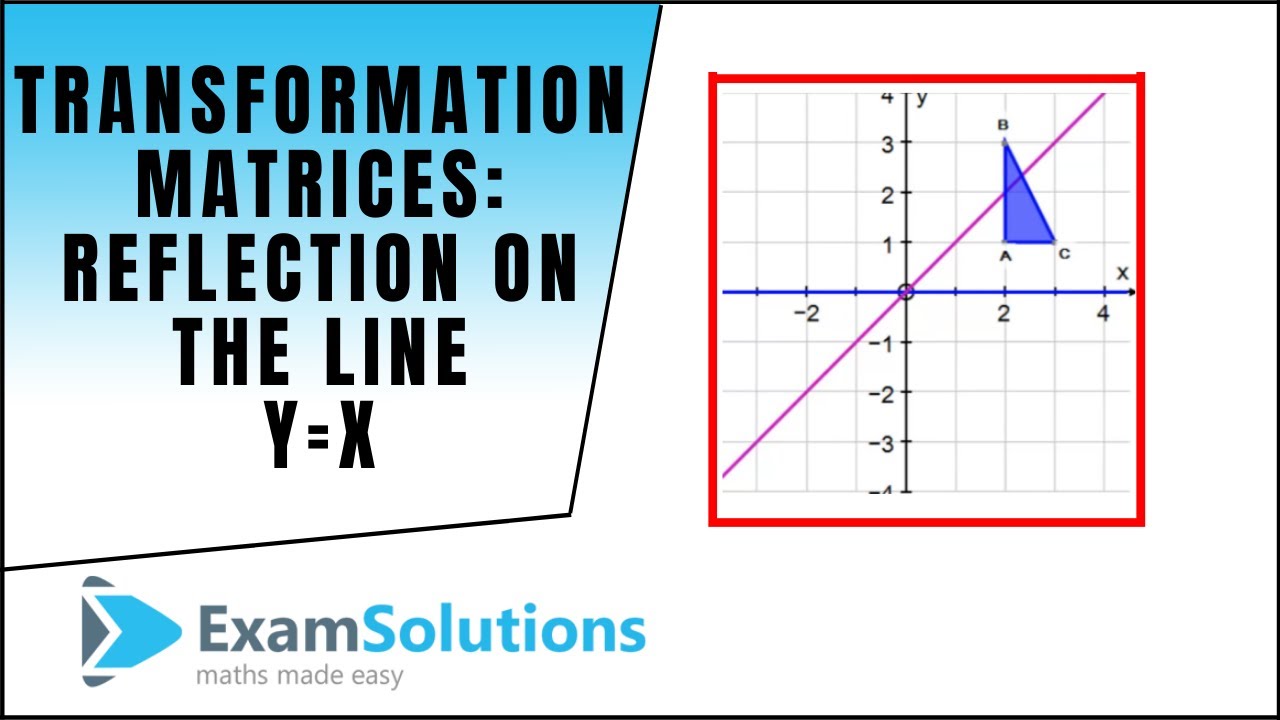
Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube
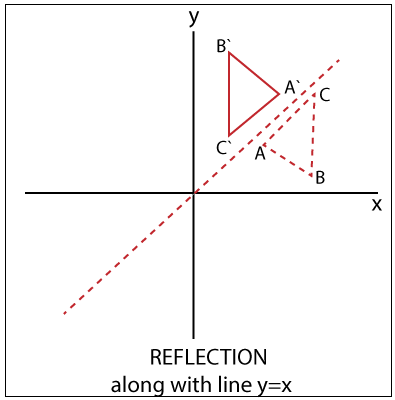
Reflection in line y=x matrix
Reflection in line y=x matrix-Related Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?Matrices for Reflections 257 Lesson 46 This general property is called the Matrix Basis Theorem Matrix Basis Theorem Suppose A is a transformation represented by a 2 × 2 matrix If A (1, 0) → (x 1, y 1) and A (0, 1) → (x 2, y 2), then A has the matrix x 1 x 2 y 1 y 2 Proof Let the 2 × 2 transformation matrix for A be ab
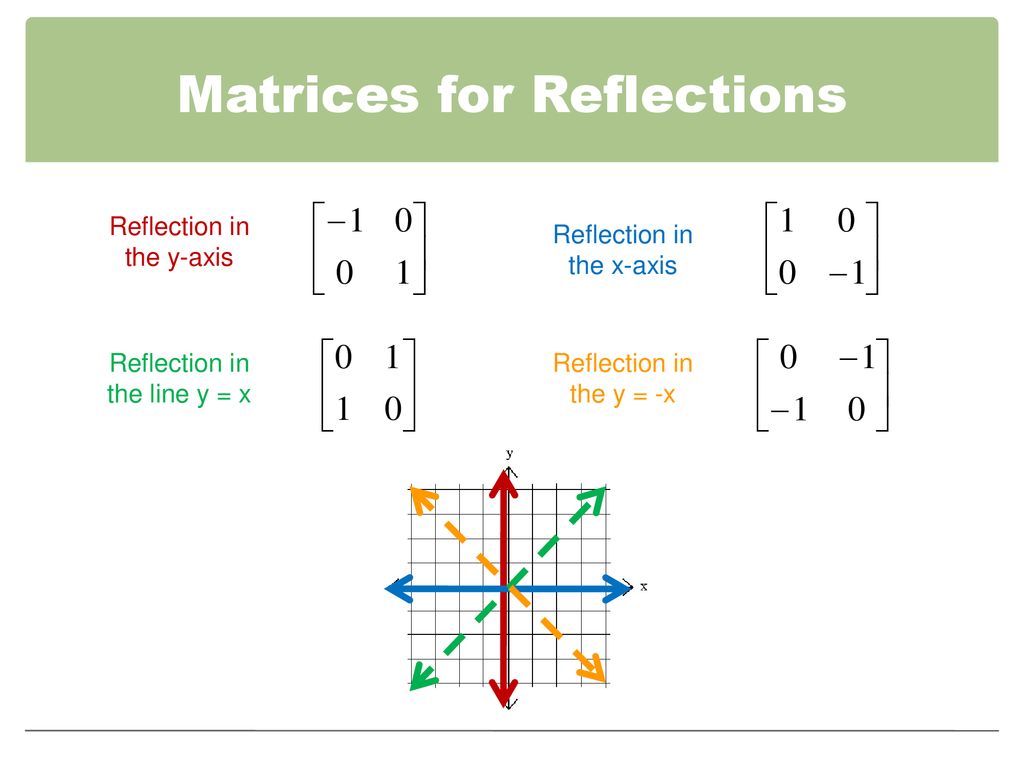



4 4 Geometric Transformations With Matrices Ppt Download
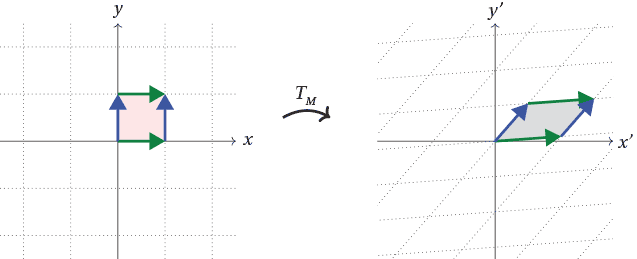
What is the 2x2 matrix that is a reflection across the line y= 2x? I know the matrix for the reflection across the line y = x in 2 Dimensions is $$ \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} $$ I am not sure how to find the matrix for the reflection in 3 DimensionsOr the columns in my identity matrix But a general theme is any of these transformations that literally just scale in either the x or y direction, and when I or, well, you could say, scale They can either shrink or expand in the x or y direction Or flip in the x or y direction, creating a reflection These are going to be diagonal matrices
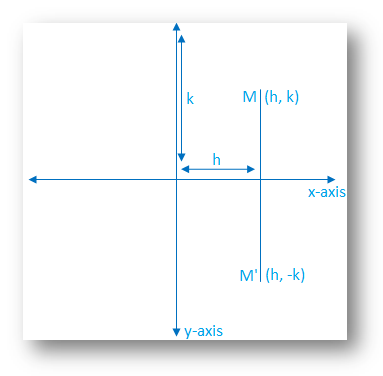
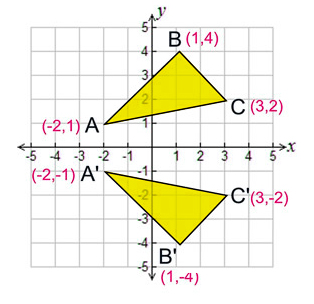
Note that this matrix is symmetrical about the leading diagonal, unlike the rotation matrix, which is the sum of a symmetric and skew symmetric part Simple cases In order to check the above lets take the simple cases where the point is reflected in the various axis Reflection in yzExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Previous question Next questionReflect over the xaxis When you reflect a point across the xaxis, the xcoordinate remains the same, but the ycoordinate is transformed into its opposite (its sign is changed) If you forget the rules for reflections when graphing, simply fold your paper along the xaxis (the line of reflection) to see where the new figure will be located Or you can measure how far your points are away
Matrices In Motion Reflection Animation Project Input up to 10 shape (x,y) coordinates below X Y Click any button below to multiply the above matrix by the shown reflection matrix xaxisRequired Supplemental Exercise (2 pts) Write the matrix that represents a reflection across the line y = x in R2 Determine the eigenvalues and eigenvectors, either through direct calculation or by thinking about which vectors will be sent to themselves or to a scalar multiple of themselves Then geometrically describe each eigenspaceGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



1
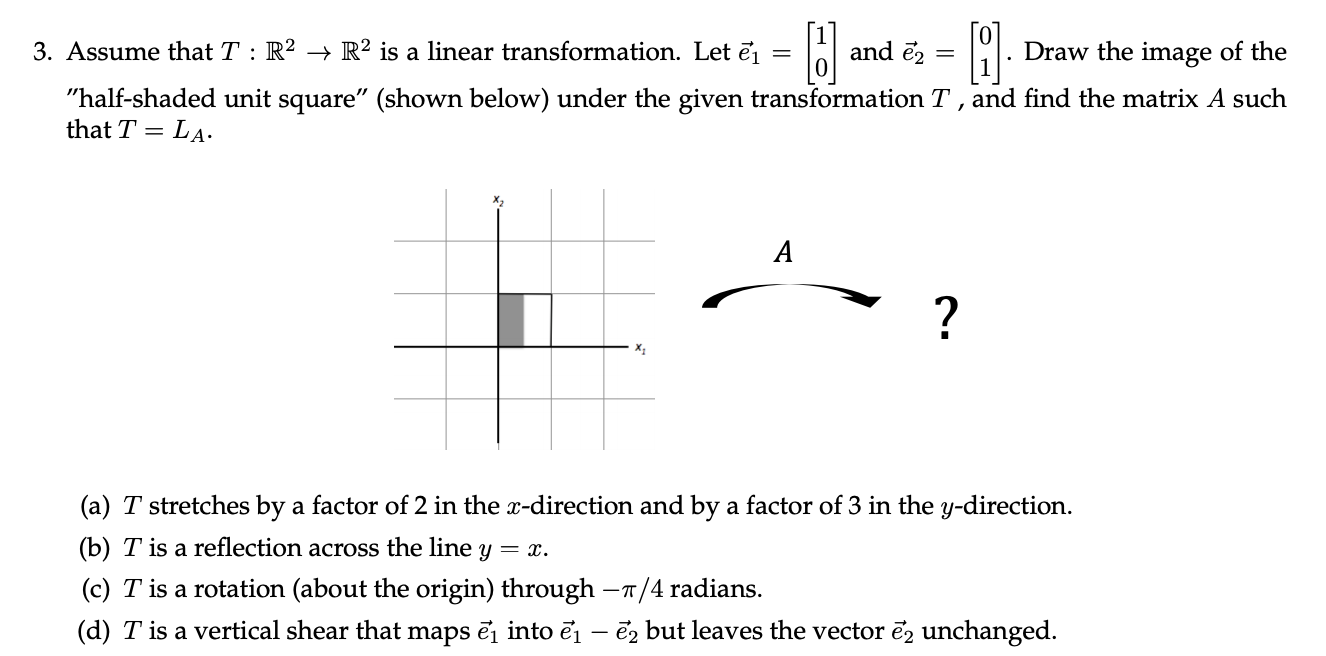



Solved 3 Assume That T R2 R2 Is A Linear Chegg Com
This video explains what the transformation matrix is to reflect in the line y=x This video explains what the transformation matrix is to reflect in the line y=x The formula for a line in two dimensions through the origin looks like this y = m x Using m (slope) in that formula, a reflection matrix looks like this R = 1 1 m 2 1 − m 2 2 m 2 m m 2 − 1 Check out this article for information on Householder transformation if you want to dive into the derivation of this formula Let T R 2 → R 2 be a linear transformation that maps the line y = x to the line y = − x Note that the linear transformation T is completely determined if the values of T on basis vectors of the vector space R 2 are known Let B = { 1 0, 1 1 }



Bestmaths




Write The Matrix Equation For The Identity Isometry Chegg Com
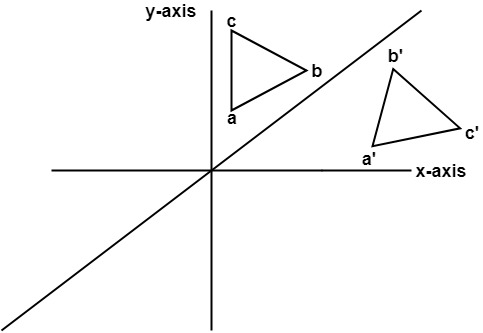
Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you want Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution a I found T = 0 11 0 b Reflection across a line of given angle Let x,y 𝐱, 𝐲 be perpendicular unit vectors in the plane Suppose we want to reflect vectors (perpendicularly) over a line that makes an angle θ θ with the positive x 𝐱 axis More precisely, we are given a direction direction vector u =cosθxsinθy 𝐮




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Solved Find The Matrix For The Linear Transformation Which Chegg Com
Expert Answer Who are the experts? Reflection about the line #y = x# The effect of this reflection is to switch the x and y values of the reflected point The matrix is #A = ((0,1),(1,0))# Reflection In 2D Graphics Reflection deals with obtaining a mirror image of the 2D object About x=y line To do this move x=y line to any of the axis In the given diagram the angle of rotation is 45 o as the points are plotted as (0, 0), (1, 1), (2, 2), and so on Imposing the line clockwise (45 o) imposing it on the xaxis we have,




Reflection Over X Axis Y Axis Equations Examples Graph Video Lesson Transcript Study Com




Transformation Using Matrices Geometry Transformations Mathplanet
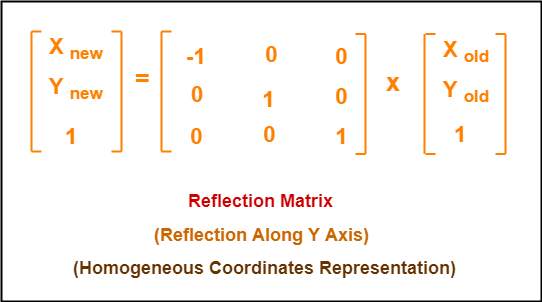
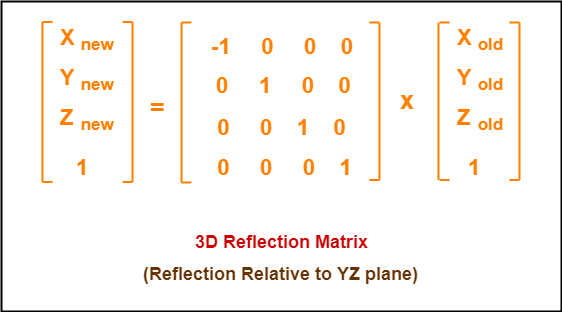
Properties of Parallel Lines by Erin Larson 91 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over y=x reflection over the line y=x Reflection over y=x We can represent Reflection by using the following three waysReflection along with xy Plane In the xy plane reflection, the value of z is negative x 1 = x 0 y 1 = y 0 z 1 = z 0 Matrix of 3D ReflectionReflection along with xz Plane In the xz plane reflection the value of y is negative x 1 = x 0 y 1 = y 0 z 1 = z 0 Matrix of 3D In order to reflect the graph of an equation across the yaxis, you need to pick 3 or 4 points on the graph using their coordinates (a, b) and plot them as (



2




Ixl Transformation Matrices Write The Vertex Matrix Precalculus Practice
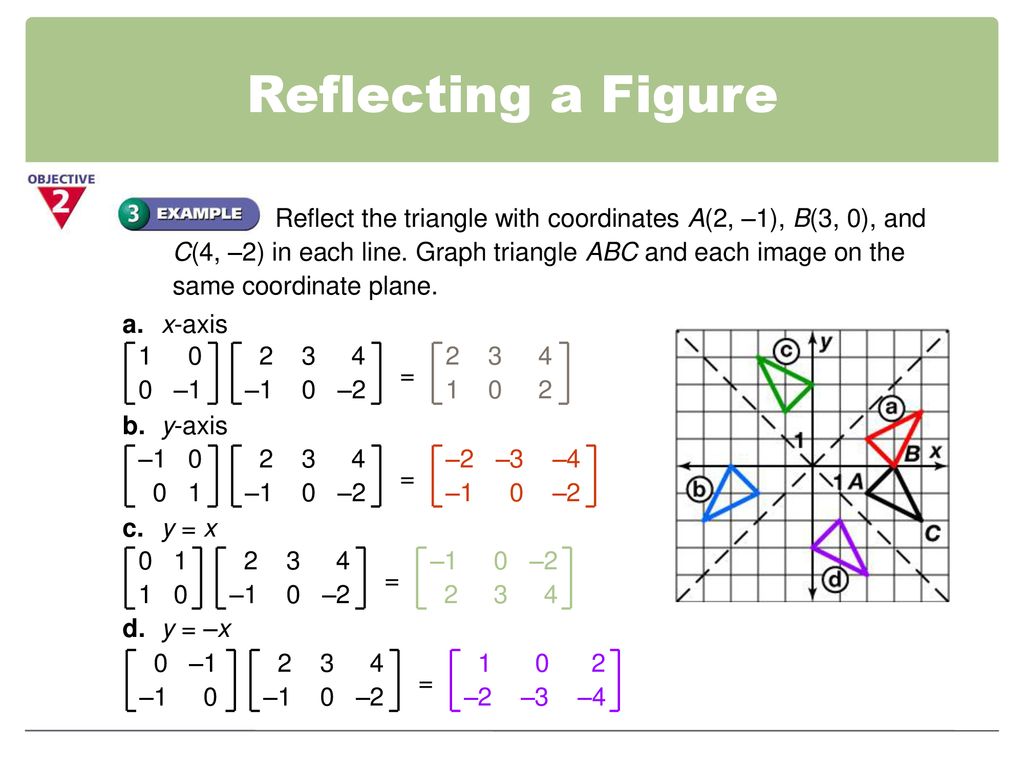
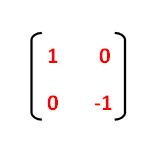
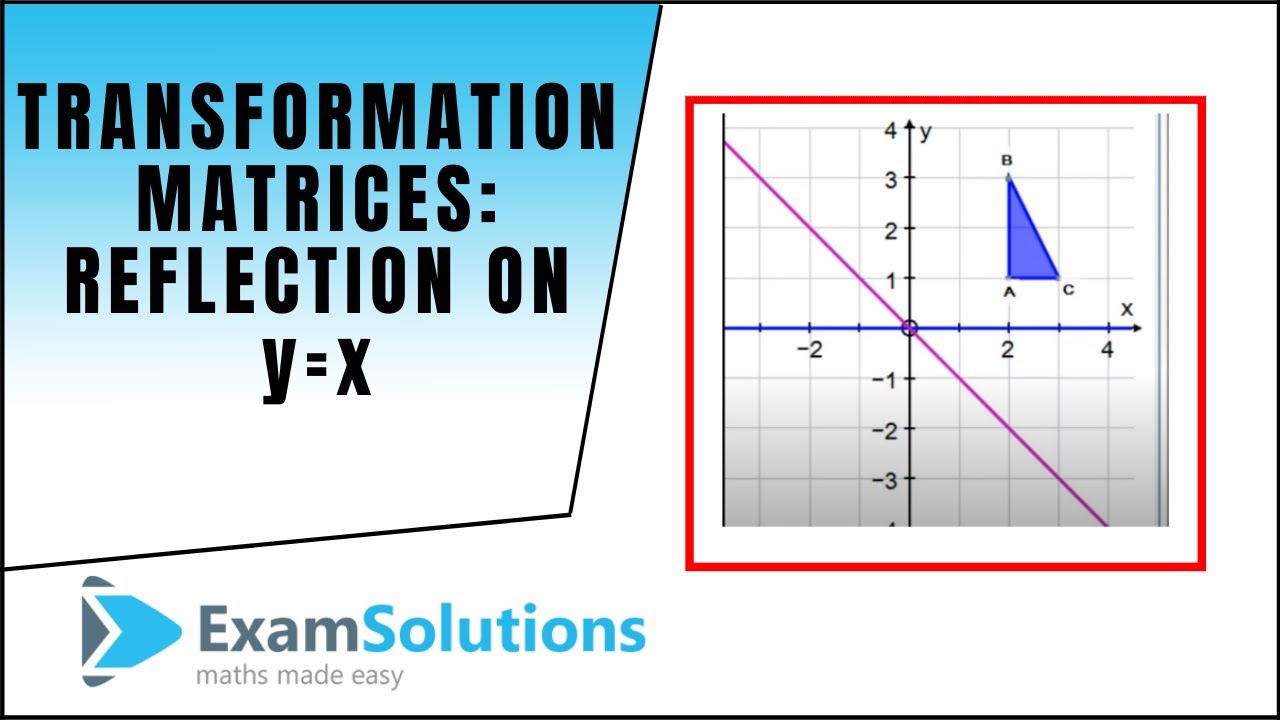
Tutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT The formula for this is {eq}(x,y) \rightarrow (x,y) {/eq} To reflect an equation over the xaxis, simply multiply the output variable by negative one {eq}y=f(x) \rightarrow y=f(x) {/eq}3 ⋅ x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 When we want to create a reflection image we multiply the vertex matrix of our figure with what is called a reflection matrix The most common reflection matrices are for a reflection in the xaxis 1 0 0 − 1 for a reflection in the yaxis − 1 0 0 1




Match Each Type Of Vector Reflection With The Matrix Used To Achieve It Brainly Com



4 4 Geometric Transformations With Matrices Ppt Download
The matrix representation for a reflection in the line y = mx New Resources Angle btw line and plane, dihedral angle;In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and C Reflection along xy plane The Reflection transformation matrix is used to perform the reflection operation over the 3D image, which is as follows Consider, a point P x, y, z which is in 3D space is made to reflect along XY direction after reflection P x, y, z becomes P' x' ,y' ,z' 2 Reflection along the YZ plane This is



1



Computer Graphics Reflection Javatpoint
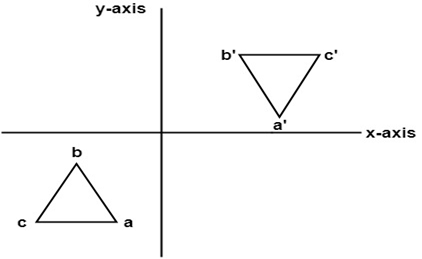
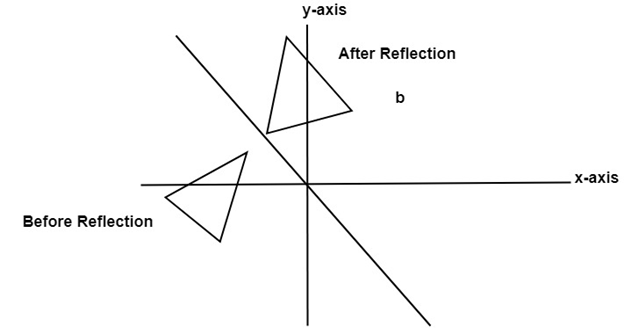
In a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3 In either case the vector − m 1 is on the perpendicular line Thus, by the reflection across the line y = m x, this vector is mapped to m − 1 That is, we have (**) A − m 1 = m − 1 It follows from (*) and (**) that A 1 − m m 1 = A 1 m A − m 1 = 1 m m − 1⇒ A reflection in the line y = x (ie a diagnoal line sloping upwards through the origin) is represented by the matrix \( \begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix} \) and has invariant line with equation y = x ⇒ A reflection in the line y = x (ie a diagnoal line sloping downwards through the origin) is represented by the matrix



2d Reflection In Computer Graphics Definition Examples Gate Vidyalay




Reflection Rules How To W 25 Step By Step Examples
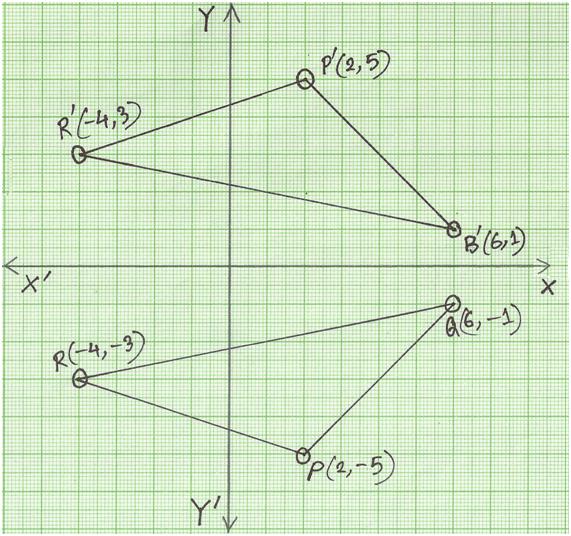
Reflection Across Y=x Reflection Across Y=x Matrix Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflectionProblem 1 Find a linear transformation rule of the form (p, q) → (r, s) such that the reflection image of the point (p, q) over the oblique line y = mx b is the point (r, s) In the general case, both r and s are functions of p, q, m and bA Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The image below shows a general Cartesian coordinate being reflected in the line y = −x




Which Vector Matrix Represents The Reflection Of The Vector Lt 1 5 Gt Across The Line X Y Brainly Com




Reflection Transformation Matrix
Step 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 3 Now, let us multiply the two matrices Step 4The linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (m I solved Cx = e1, Cx = e2, Cx = e3 (I checked these x's a few times so I am pretty confident about this part) Then I put these x's as the column vectors of a matrix and switched the sign of the last row (again thinking this was writing the reflection of the standard basis across the plane in terms of B) This yielded 18 36 08 4 10 10



Content Linear Transformations And Matrices



3d Reflection In Computer Graphics Definition Examples Gate Vidyalay
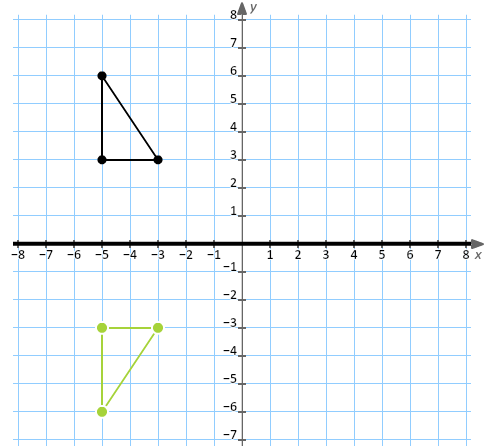
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicA reflection can be done through yaxis by folding or flipping an object over the y axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directions As you suggest, make the change of variables ( X, Y) = ( x − 2, y − 3) The matrix of the rotation in ( X, Y) coordinates is 1 / 2 − 3 / 2 3 / 2 1 / 2 In ( x, y) coordinates, we have x y 1 / 2 − 3 / 2 3 / 2 1 / 2 x − 2 y − 3 2 3 = 1 / 2 − 3 / 2 3 / 2 1 / 2 x y 1 3 3 / 2 3 / 2 − 3




Matrix Reflections Youtube




Reflection Definition Reflection In The Coordinate Plane
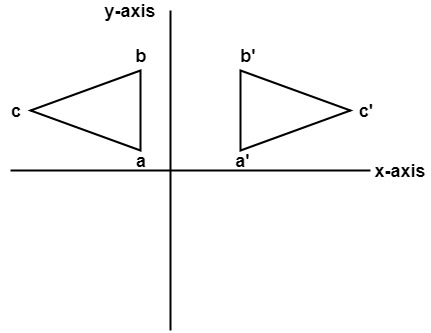
Apply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)Gives a reflection in the line $y=x\tan\theta$ The point $P''=(p'',q'')$ is the image of the point $P'$ after reflection in the line $y=x\tan\phi$ Apply the transformation $$T_2' = \left( \eqalign{\cos 2\phi &\sin2\phi \\ \sin2\phi & \cos2\phi}\right)$$ to the point $P'=(p',q')$ to find the coordinates of the point $P''$ in terms of $p, q, \theta$ and $\phi$




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Solved We Can Examine The Reflective Symmetries By Finding A Chegg Com
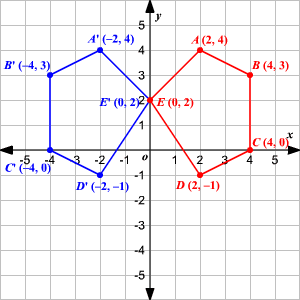
The line of reflection is a line along which an image reflects Reflection of point using graph paper is described as a figure that is built around a single point It is also known as a point of reflection or its centre Reflection on graph paper (on the cartesian place) is for \ (X\) and \ (Y\) axis If a figure is stated to mirror anotherUnder a reflection in the line y = x the point is transformed to Thus Expand this matrix equation to yield two linear equations These equations are valid for all choices of p and q What happens when p = 0 and q = 1?



Reflection Of A Point In X Axis Reflection Of A Point Reflection




Reflection A Transformation That Uses A Line To Reflect An Image A Reflection Is An Isometry But Its Orientation Changes From The Preimage To The Ppt Download




Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




The Useless Perspective That Transformed Mathematics Quanta Magazine



Reflection Transformations Mathonline



Computer Graphics Reflection Javatpoint




4 4 Geometric Transformations With Matrices Ppt Download



What Does It Mean To Reflect Over The Y X Line Quora




Solved 0 Apply The Transformation Matrix To The Vector 1 0 Chegg Com



Reflection Transformation Matrix




Ceaseless Learning Reflection In Line Y Mx Matrix



What Is The Reflection Over The Y Axis Of The Point 4 7 Quora



Computer Graphics Reflection Javatpoint



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs




Reflection Definition Reflection In The Coordinate Plane



Reflection Of A Point In X Axis Reflection Of A Point Reflection




How To Reflect A Line Segment Across The X Axis Or Y Axis Geometry Study Com



Reflection In A Cartesian Plane Lexique De Mathematique



Reflection In 2d Graphics Geeksforgeeks
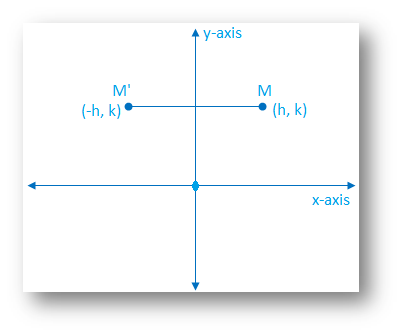



Reflection Of A Point In Y Axis Reflection Of A Point Reflection




Find Standard Matrix Of Linear Transformation Is This Right Mathematics Stack Exchange




Reflection Transformation Matrix
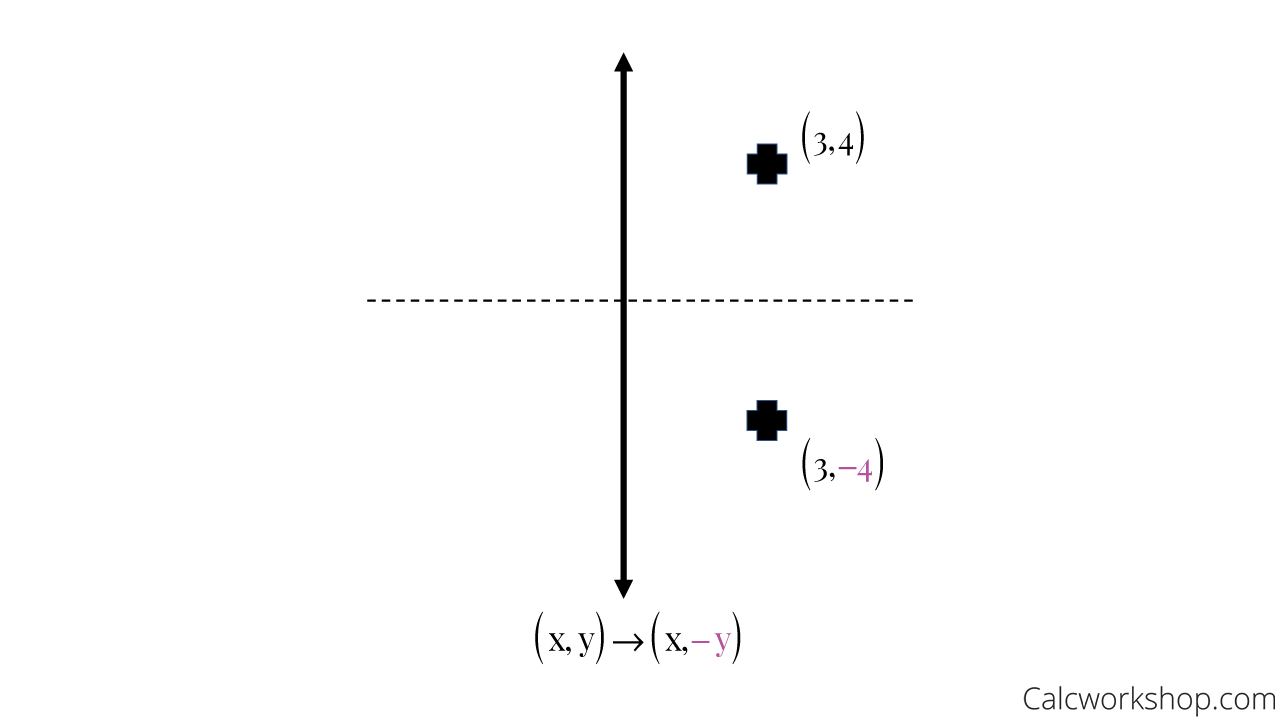



Reflection Rules How To W 25 Step By Step Examples



Casioeducation Files Wordpress Com
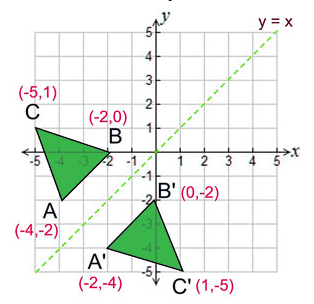



Reflection Definition Reflection In The Coordinate Plane




Matrix Transformation




Match Each Type Of Vector Reflection With The Matrix Used To Achieve It Brainly Com



2




Give 3d Transformation Matrix For 1 Translation 2 Scaling 3 Rotation 4 Reflection 5 Shear



Computer Graphics Reflection Javatpoint




Reflecting Shapes Article Reflections Khan Academy




Reflection Transformation Matrix




Reflection Over X Axis Y Axis Equations Examples Graph Video Lesson Transcript Study Com




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



2



Math Alive Geometry 1




Linear Transformation Examples Scaling And Reflections Video Khan Academy




Solved Point Match Each Linear Transformation With Its Matrix 0 5 0 5 Rotation Through An Angle Of 90 In The Clockwise Direction B Reflection In The Line Y X C Projection Onto The Y Axis



Linear Transformation Examples Scaling And Reflections Video Khan Academy




Answered Q8 Consider I W E R As Below Where Bartleby



2



Reflection Definition Reflection In The Coordinate Plane



Transformation Of Graphs Using Matrices Reflection




Transformations Animated Gifs Reflections Rotations Translations Dilations And Isometries
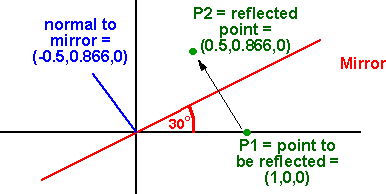



Maths Reflection Using Matrix Martin Baker




The Matrix For The Linear Transformation Of The Reflection Across A Line In The Plane Problems In Mathematics




The Vector 6 5 Is Reflected Across The Y X And The Resulting Matrix Is Dilated By A Scale Of 1 5 Brainly Com



Matrix Reflections
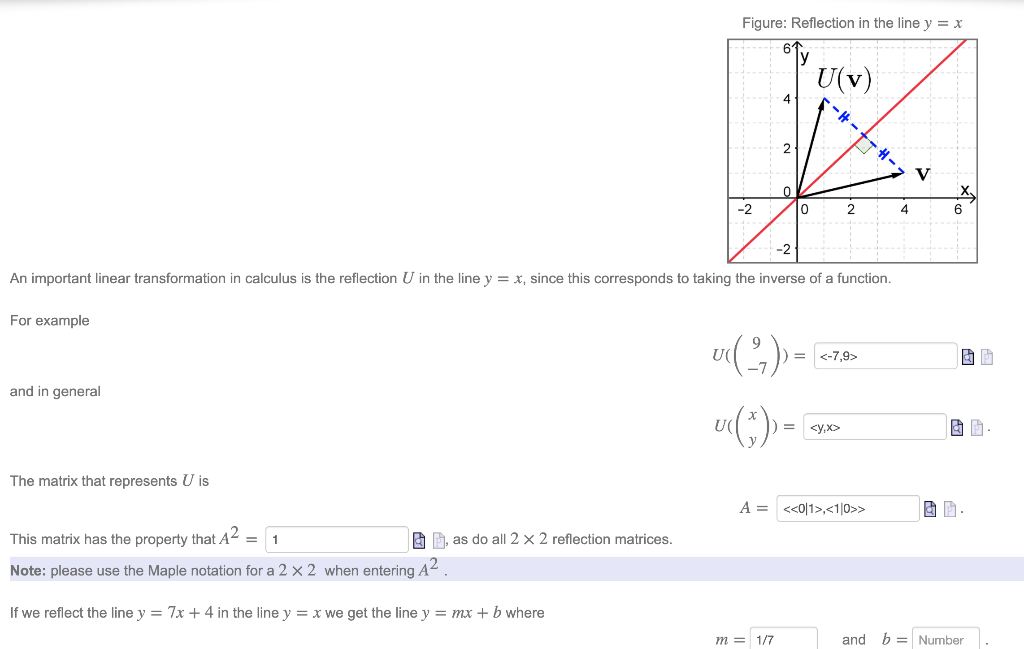



Solved Figure Reflection In The Line Y X 61 U V 4 2 Chegg Com




Solved 2 16 Points We Are Looking For The Matrix Of The Linear Transformation T R2 R Which Is The Reflection Across The Line Y 3x 4 Let S Find That Matrix Step By



Reflection Transformations Mathonline



Math Alive Geometry 1




Reflection Rules How To W 25 Step By Step Examples




Solved 3 6 Points Let T R2 3 R Be The Linear Transformation Defined By Reflection Across The Line Y And Let A Be The Standard Matrix Of A A Sketch




12 Tuesday



1
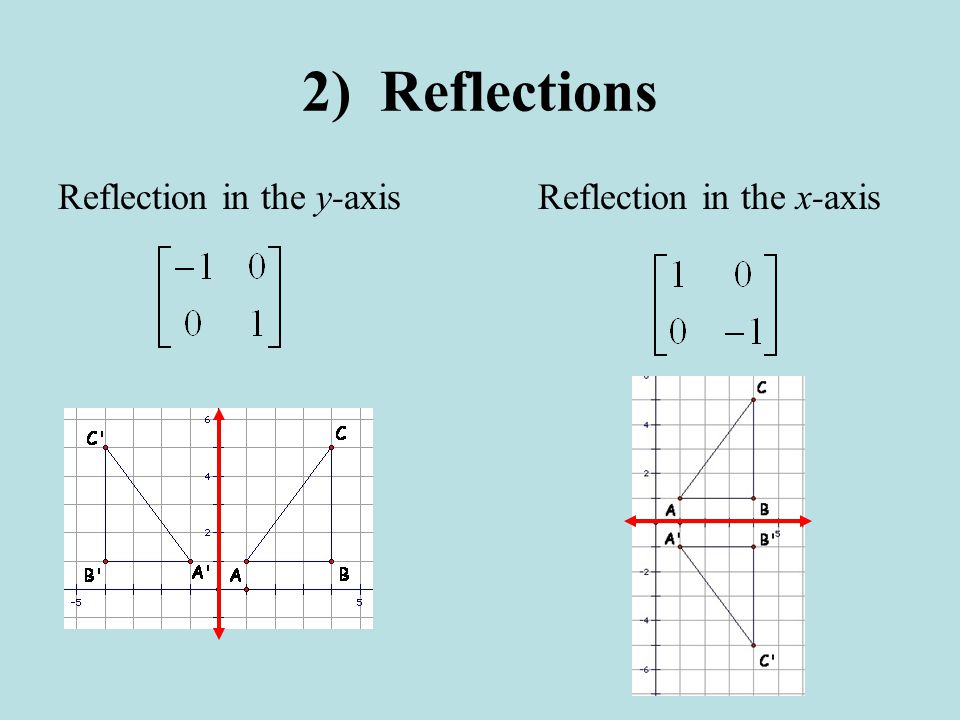



4 4 Transformations With Matrices Ppt Video Online Download
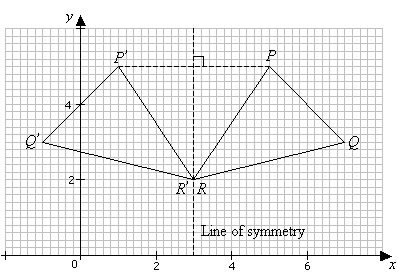



Reflection Transformation Solutions Examples Videos



Computer Graphics Reflection Javatpoint




Reflection In The Line Y X Transformation Matrix Youtube




Reflections



Cs 1110 Assignment 5




Reflection Transformation Matrix




How To Reflect A Polygon Over A Horizontal Line Geometry Study Com



Solved Find The Standard Matrix For The Reflection Of R 2 About The Stated Line And Then Use That Matrix To Find The Reflection Of The Given Point About That Line The Reflection Of




Reflection Rules How To W 25 Step By Step Examples




Matrix Transformations Questions Pdf Pdf



2d Reflection



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




Solved A Find The Matrix Of Reflection Across The Line Y Chegg Com




Solved Let T R2 R2 And S R2 R Be The Linear Transformations Given By Reflection Across The Y Axis T And Reflection Across The Line Y X S A Find The



Does Reflecting The Parabola Across The X Axis Change The Axis Of Symmetry Quora
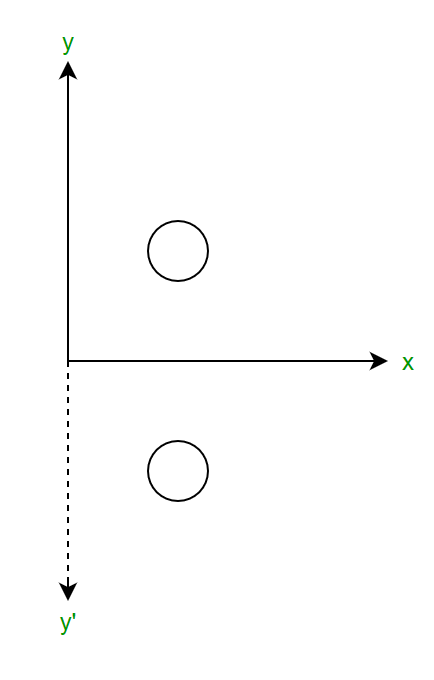



Reflection In 2d Graphics Geeksforgeeks



1
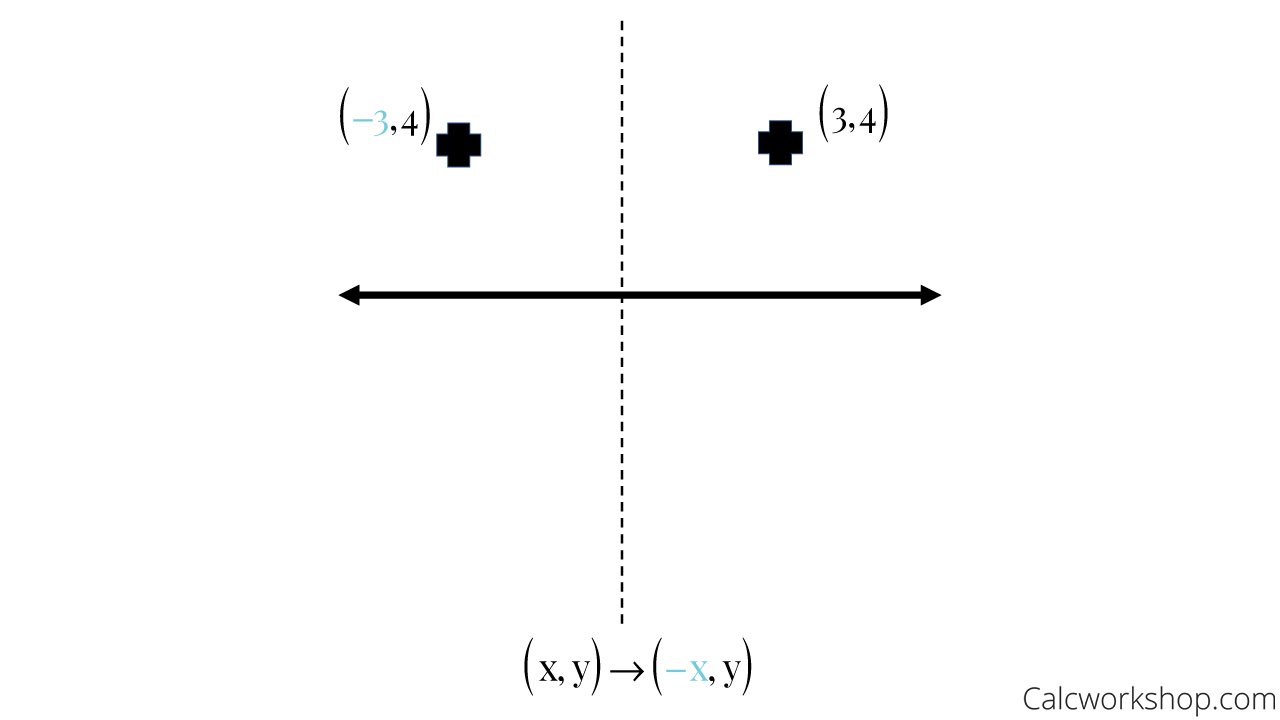



Reflection Rules How To W 25 Step By Step Examples
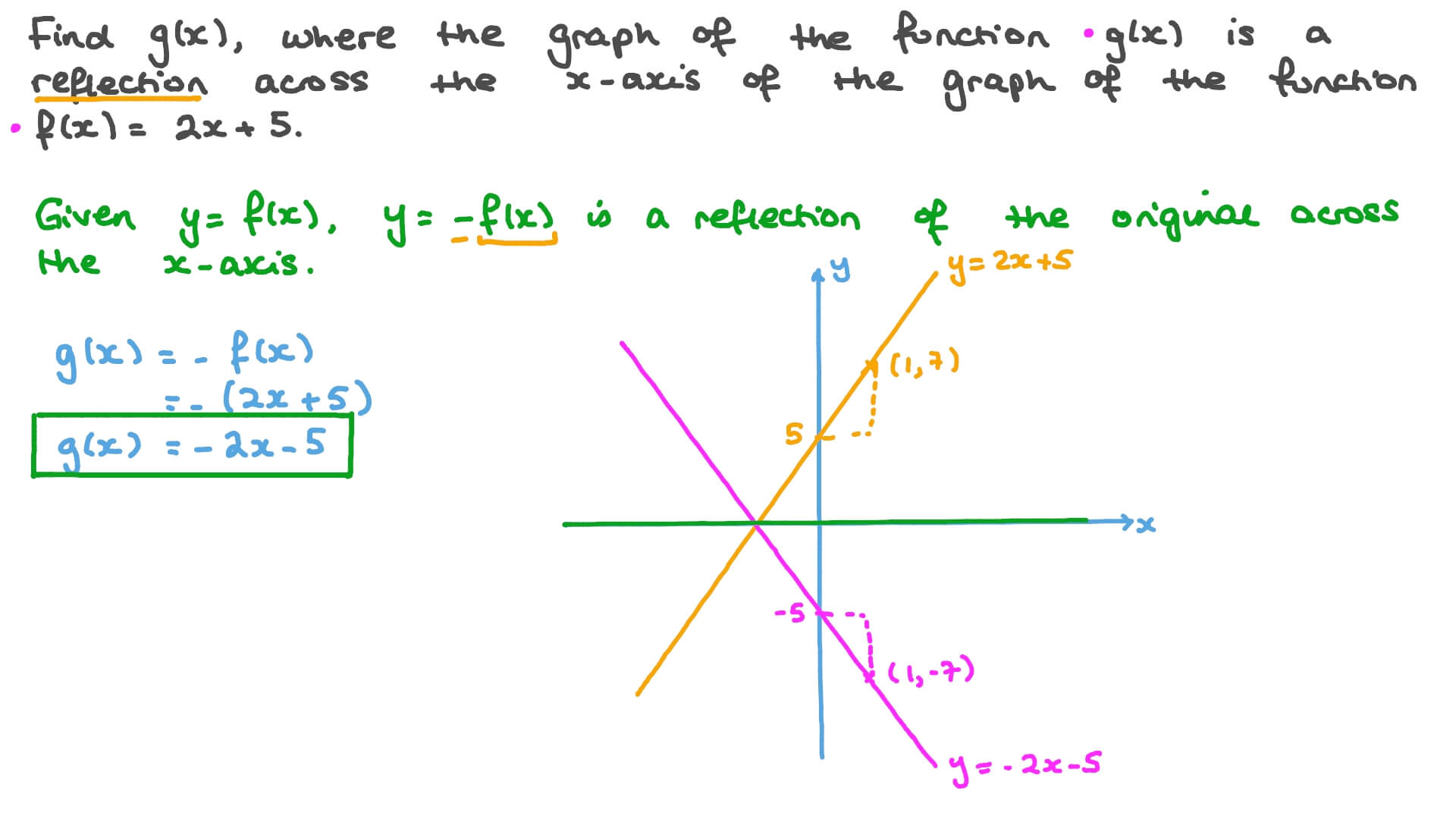



Question Video Identifying The Equation Of A Graph After A Reflection Nagwa




Linear Algebra Find The Standard Matrix For F R3 To R3 The Reflection Across The Plane H X 2x Y Z 0 Mathematics Stack Exchange
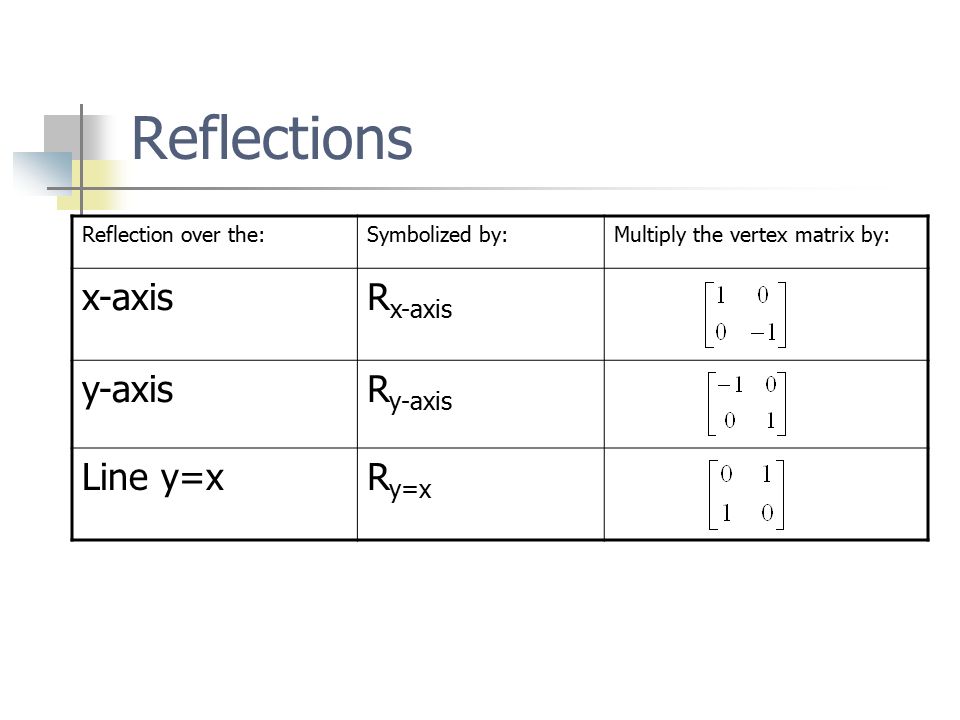



2 4 Modeling Motion With Matrices Pre Calc A Vocabulary Transformations Translation Reflection Rotations Dilations Ppt Download
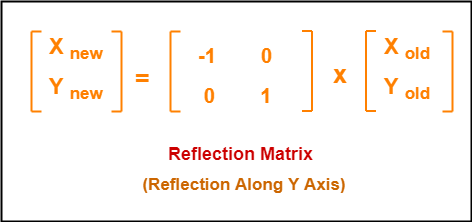



2d Reflection In Computer Graphics Definition Examples Gate Vidyalay



0 件のコメント:
コメントを投稿