The following 13 multiple choice questions are worth 5 points each 1 List the transformations needed to transform the graph of y = f (x) to the graph of a Shift to the right 1 unit, reflect about the xaxis and shift down 3 units b Shift to the right 1 unit, reflect about the xaxis and shift up 3 The graph of y=x^22x1 is translated by the vector (2 3)The graph so obtained is reflected in the xaxis and finally it is stretched by a factor 2 parallel to yaxisFind the equation of the final graph is the form y=ax^2bxc, View more similar questions or ask a new questionFind the equation of the resulting graph, if we move y = x 2 4x3 to the right side by 3 units and downwards by 2 units Solution Let f (x) = x 2 4x3 We can rewrite the equation using completing the square method f (x) = (x2) 2 7 y2 = f (x3) = (x1) 2 7 = x 2 2x8 x 2 2x8 is the required equation Related videos 7,9 1,11,760

Content Transformations Of The Parabola
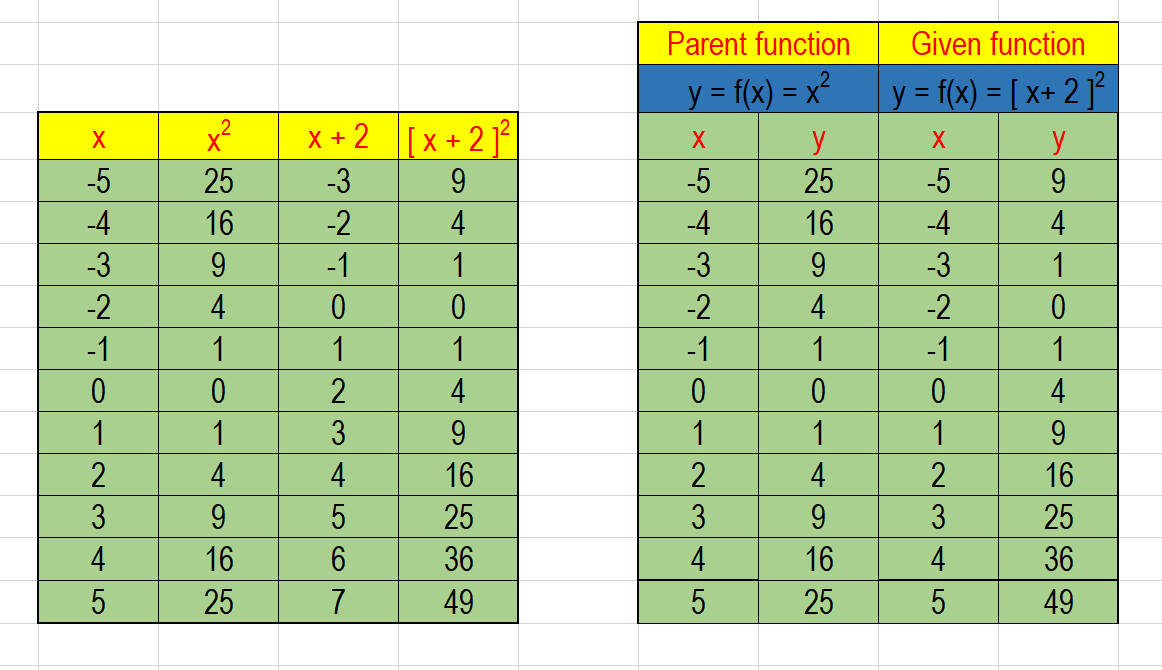
Graph of y=x^2 transformations
Graph of y=x^2 transformations-The graph of a function may stretched or compressed horizontally or vertically, and it may be shifted up or down, and left or right The graph may also be reflected in either or both of the coordinate axes If f is a function, then the graph of y = f ( x) is the graph of y = f ( x) reflected in the y axis, and the graph of y = f ( x) is theLet us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;
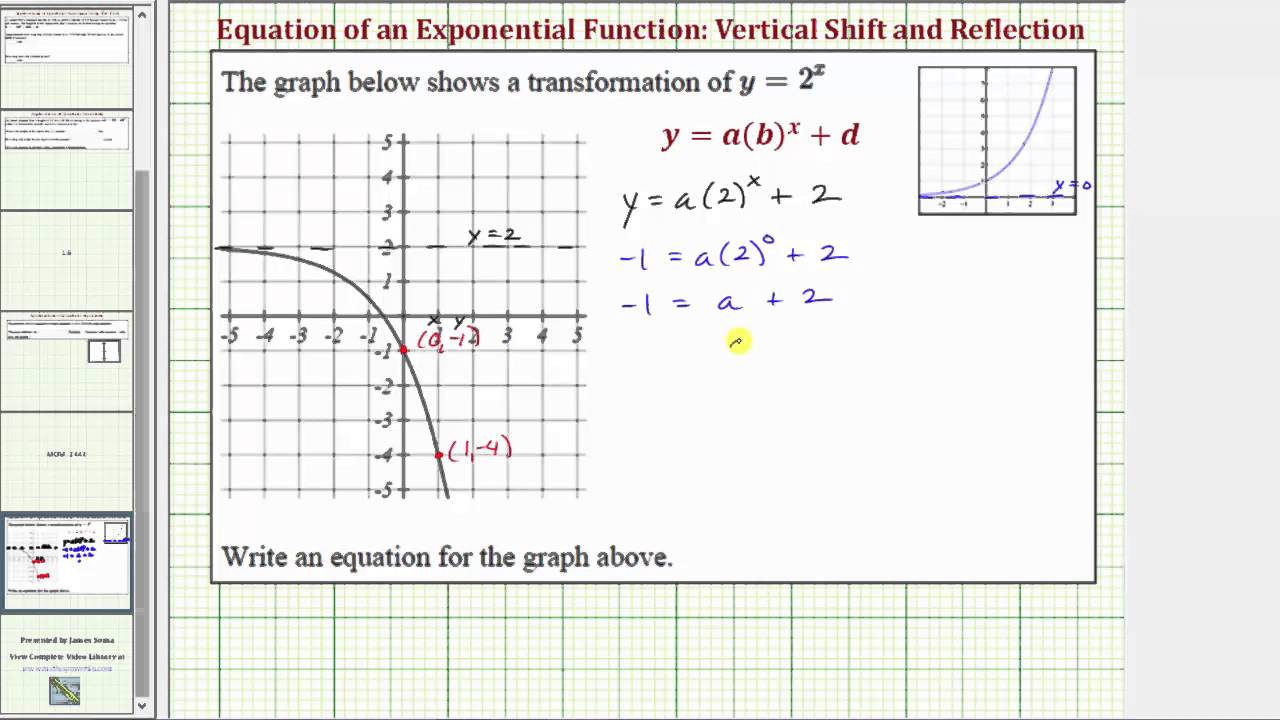



Ex Determine The Equation Of A Transformation Of Y 2 X Youtube
Transformations of the Sinusoidal Graph By Lacy Gainey We are going to examine the graphs of y = a sin(bx c) for different values of a, b, and c and explore the impact of each of these parameters Before I have students examine transformations of the sinusoidal graph, I will have them examine transformations of the function for a review Review Graph the followingGraph Transformations A transformation is something that is done to a graph/function that causes it to change in some way This topic is about the effects that changing a function has on its graph There are two types of transformation translations and reflections, giving 4 key skills you must be familiar with Throughout this topic, we will use the notation f(x) to refer to a function2 Horizontaland Vertical Stretches, Compressionsand Reflections 6 Transforming f(x) = √ xinto g 1(x) = − √ x The graph of y= g 1(x) is in Figure 6It is obtained by the following transformations
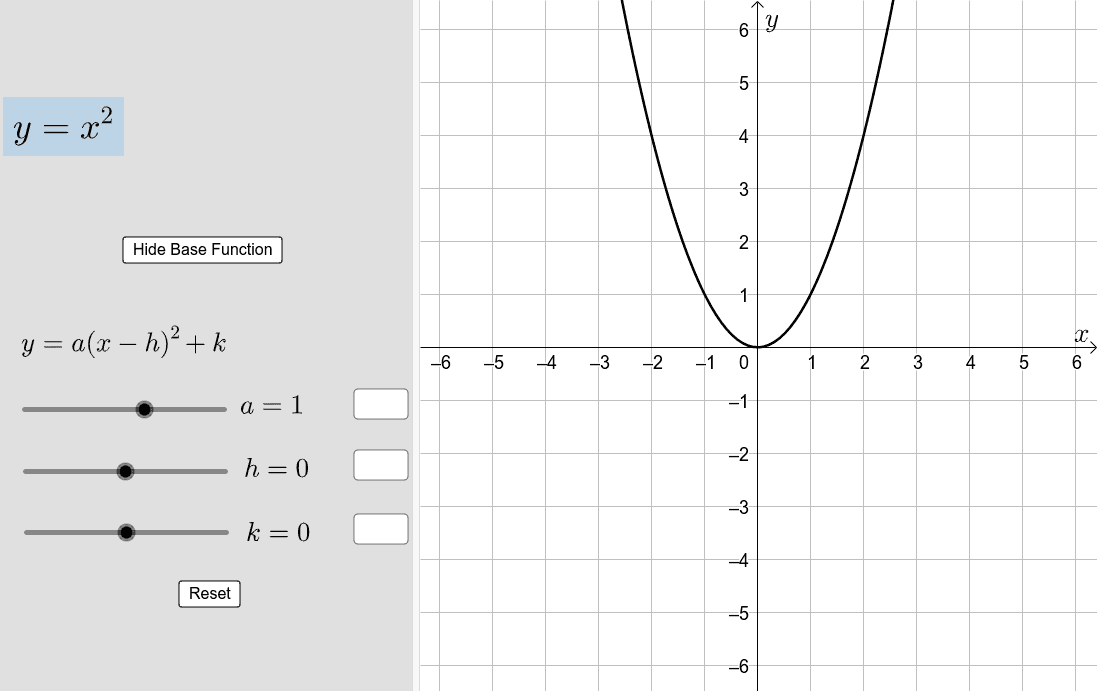
MATH 115 09F _ EXAM 2White _ Paeelof?Combining Vertical and Horizontal Shifts Now that we have two transformations, we can combine them Vertical shifts are outside changes that affect the output (y) values and shift the function up or downHorizontal shifts are inside changes that affect the input (x) values and shift the function left or rightCombining the two types of shifts will cause the graph of a function to shift upIt can be expedient to use a transformation function to transform one probability density function into another As an introduction to this topic, it is helpful to recapitulate the method of integration by substitution of a new variable x2 = 4y(2−y) x = 2 p y(2−y) – 114 Parabola, Geometric Transformations Move the sliders 'a' 'h' and 'k' to explore the transformations applied to the
Many students have difficulty with the graph transformation of oblique asymptote Consider the oblique asymptote y = x1 (red line) i) To start, let's consider the quadratic function y=x2 Its basic shape is the redcoloured graph as shown Furthermore, notice that there are three similar graphs (bluecoloured) that are transformations of the original g (x)= (x5)2 Horizontal translation by 5 units to the right h (x)=x25 Vertical translation by 5 units upwards i (x)= (x)2 Functions can get pretty complex and go through transformations, like reflections along the x or yaxis, shifts, stretching and shrinking, making the usual graphing techniques difficult We'll show you how to identify common transformations so you can correctly graph transformations of functions




Graph Y X 2 3 Youtube



1
When x is zero, they're going to give us the same value So they're both going to have the same yintercept And so are graph is going to look like, our graph is going to look something like, this They're going to be mirror images flipped around the yaxis So, it's going to look like that That is the graph of y is equal to two to the negative xView my channel http//wwwyoutubecom/jayates79Since the positive constant is greater than one, the graph moves away from the xaxis 2 units (iii) y = x 1 Since 1 is added to the function, we have to translate the graph of y = x 1 unit upward (iv) y = (1/2)x 1 Step 1 Since 1/2 is multiplied by x, we have to perform translation



The Graph Shown Below Results From Transformations Gauthmath




The Graph Of Y Sqrt 4x X 2 Is Given Below Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com
Graph transformation is the process by which an existing graph, or graphed equation, is modified to produce a variation of the proceeding graph It's a common type of problem in algebra, specifically the modification of algebraic equations Sometimes graphs Identify the vertex c compare with the graph of y = x^2 (state any transformations used) The function f(x) = x^2 The graph of g(x) is f(x) translated to the right 3Purplemath The last two easy transformations involve flipping functions upside down (flipping them around the xaxis), and mirroring them in the yaxis The first, flipping upside down, is found by taking the negative of the original function;
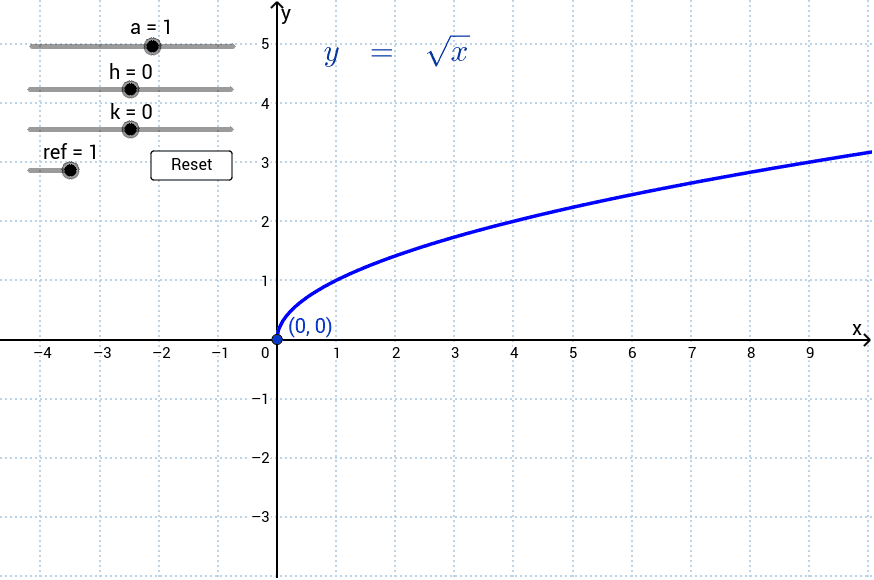



Transformations Of The Graph Y Sqrt X Geogebra



Lecture 6 Sections 2 3 And 2 7 Graphs Of Lines And Transformations
Next, reflect all points about the x axis and draw in the final graph with a solid curve General Steps for Graphing Functions using Transformations 1 Identify and graph the basic function using a dashed curve 2 Identify any reflections first and sketch them using the basic function as a guideAn activity to investigate transformations on the graph of y=x² New Resources The Cosine Function; This example uses the basic function \ (y = f (x)\) This can then be uses to draw related functions Notice that the main points on this graph are \ (x =




Content Transformations Of The Parabola



Y 1 X
Notice on the next page that the graph of (x)2 is the same as the graph of our original function x 2 That's because when you flip the graph of x over the yaxis, you'll get the same graph that you started with That x2 and ( 2x) have the same graph means thatThe x is to be multiplied by 1 This makes the translation to be "reflect about the yaxis" while leaving the ycoordinates alone y=1/2 f(x/3) The translation here would be to "multiply every ycoordinate by 1/2 and multiply every xcoordinate by 3"A graph can be translated horizontally, vertically or in both directions Translations parallel to the yaxis \ (y = x^2 a\) represents a translation parallel to the \ (y\)axis of the graph of \
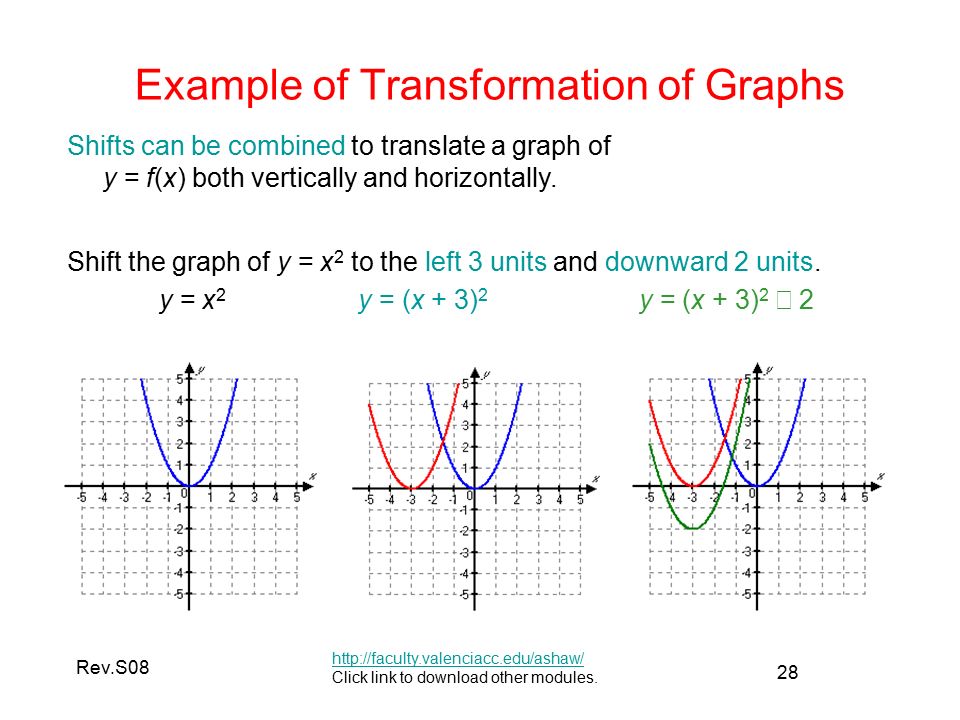



Transformation Of Graphs Ppt Video Online Download




Transformation Of Graphs Y F X Into Y 2f X 1 Quick Explanation Youtube
See the answer See the answer done loading Use the graph of y=2^x and transformations to sketch the exponential function Determine the domain and range Also, determine the yintercept, and find the equation of the horizontal asymptote f (x)=2^x3 If they had stated the problem in words, it might have read thus The graph of function f is a transformation of the function y = x^2 for which the vertex , (0, 0) in the parent function, transforms to (2, 1), and the point (1, 1) transforms to (1, 1) That's all the information you need from the pictureMixed Transformations Most of the problems you'll get will involve mixed transformations, or multiple transformations, and we do need to worry about the order in which we perform the transformations It usually doesn't matter if we make the \(x\) changes or the \(y\) changes first, but within the \(x\)'s and \(y\)'s, we need to perform the transformations in the order below



5 A The Graph Of Y Fx Is Transformed To The Graph Gauthmath




Transforming Exponential Graphs Example 2 Video Khan Academy
Lab Transformations of Absolute Value Functions Graph the following absolute value functions using your graphing calculator For each family of functions, sketch the graph displayed on graphing paper Then answer the questions given 1 Parent graph y =x y =x 2 y =x 4 y =x 8 a What do all functions in this family have in common?That is, the rule for this transformation is −f (x) To see how this works, take a look at the graph of h(x) = x 2 2x − 3In the previous example, for instance, we subtracted 2 from the argument of the function y = x2 y = x 2 to get the function f (x) =(x−2)2 f ( x) = ( x − 2) 2 This subtraction represents a shift of the function y = x2 y = x 2 two units to the right A shift, horizontally or vertically, is a type of transformation of a function




Graphing Square And Cube Root Functions Video Khan Academy




Solved 10 4 2 Graph The Function F X X 5 2 2 By Chegg Com
Transformations of Graphs Practice Questions – Corbettmaths corbettmathsThis occurs when a constant is added to any function If we add a positive constant to each ycoordinate, the graph will shift up If we add a negative constant, the graph will shift down For example, consider the functions g (x) = x 2 − 3 and h (x) = x 2 3 Begin by evaluating for some values of the independent variable x Therefore, the graph of y=f(xc) is just the graph of y=f(x) shifted c units to the right" I don't understand why it shifts to the right I referred to the last answer, and gave a little more detail Suppose you have just plotted a point (a,b) on the graph of y=f(x), and now you want to plot the same point on the graph of y=g(x)



Transforming The Graph Of Y X Geogebra
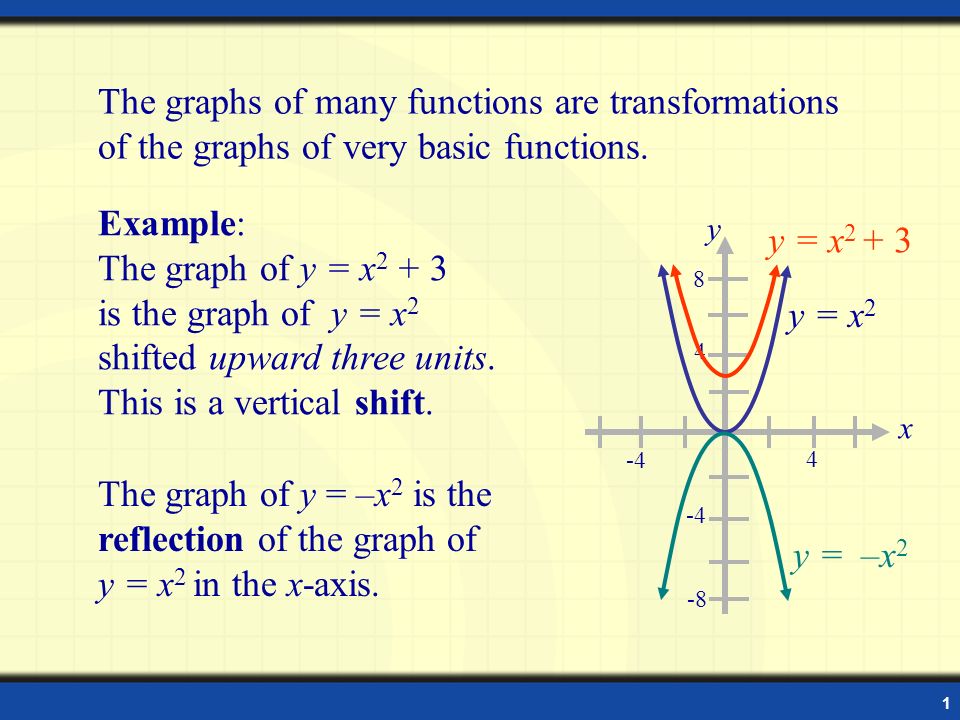



1 The Graphs Of Many Functions Are Transformations Of The Graphs Of Very Basic Functions The Graph Of Y X 2 Is The Reflection Of The Graph Of Y X Ppt Download
Describe the Transformation y=x^2 y = x2 y = x 2 The parent function is the simplest form of the type of function given y = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 y = x 2 is g(x) = x2 g ( x) = x 2 f (x) = x2 f ( x) = x 2 g(x) = x2 g ( x) = x 2Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) c y = f (x) – c Raise the graph of f by c units Lower the graph of f by c units C is added to f (x) C is subtracted from f (x) Created by UASP Student Success Centers successasueduThe second graph, y = 1 * 2^ (x3) 4, is a transformation of y = 2^x According to March11, Sal must use PEMDAS to track how y = 2^x will transform He first works with the exponent (E) A 3 was added to the x in y = 2^x, making it y = 2^ (x3) Sal transforms the graph accordingly




Transformations Of Y X Ck 12 Foundation



Solved Transformation Course Hero
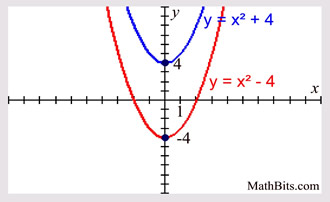
Transformations of exponential graphs behave similarly to those of other functions Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function \displaystyle f\left (x\right)= {b}^ {x} f (x) = b x without loss of shapeSection 56 Graphical Transformations In this section we are going to explore the graphical repercussions of alterations to a given function formula Specifically, we are going to explore how the graph of the function \(g\) compares to the graph \(f\) whereThis type of transformation also retains the shape of the graph but shifts it either upward or downward Let's what happens if we shift y = x 2 two units upward and downward When we translate a graph two units downward, we subtract 2 from the output value, y Similarly, we add 2 to y when we translate it two units to the upward



Quadratic Transformations Part 2 Activity Builder By Desmos




Combining Transformations Read Algebra Ck 12 Foundation
The graph of h has transformed f in two ways f(x 1) is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in f(x 1) − 3 is a change to the outside of the function, giving a vertical shift down by 3 The transformation of the graph is illustrated in Figure 159 For y = 3 log 2 x a) Use transformations of the graphs of y = log 2 x and y = log 3 x o graph the given functions b) Write the domain and range in interval notation c) Write an equation of the asymptoteA function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x 2 3 looks like this



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
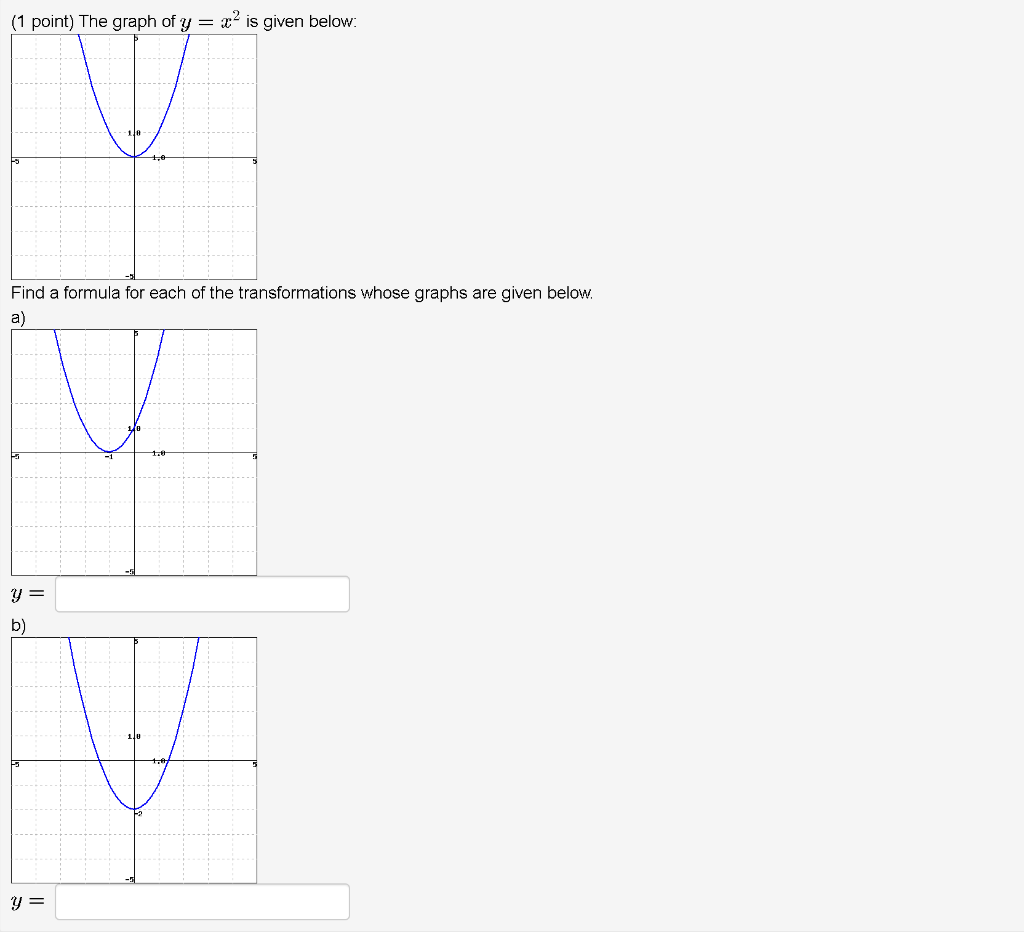



Solved 1 Point The Graph Of Y X2 Is Given Below 10 Tu Chegg Com
Sometimes by looking at a quadratic function, you can see how it has been transformed from the simple function y = x 2 Then you can graph the equation by transforming the "parent graph" accordingly For example, for a positive number c , the graph of y = x 2 c is same as graph y = x 2 shifted c units up Suppose we want to sketch the curve C and the line y=2x2 on the same graph Note how the line y2x2 is entered Adjust the Tmax to 1% more so the graph displays correctly Share this Facebook;C < 0 moves it down We can move it left or right by adding a




Transformations Of Functions Ck 12 Foundation
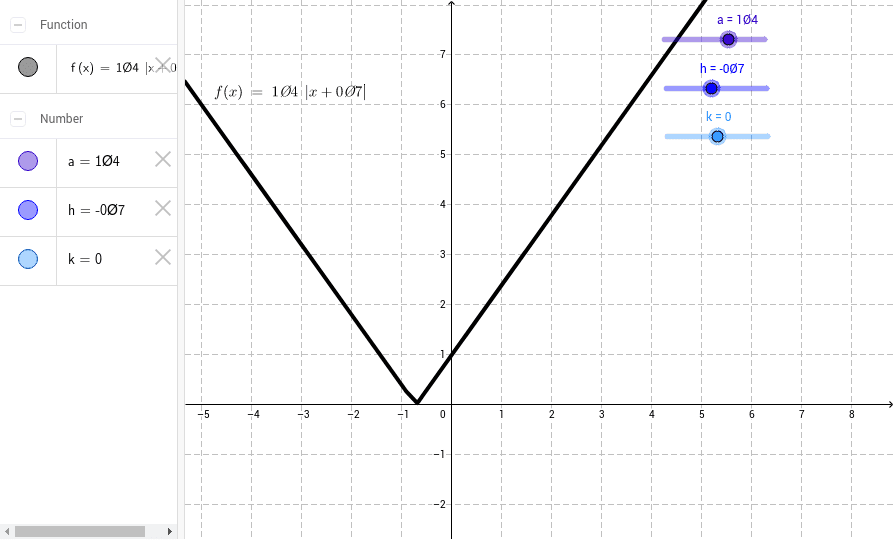



Transformations To The Graph Of Y X Geogebra
Angle btw line and plane, dihedral angle When the graph of a function is changed in appearance and/or location we call it a transformation There are two types of transformations A rigid transformation57 changes the location of the function in a coordinate plane, but leaves the size and shape of the graph unchanged A nonrigid transformation58 changes the size and/or shape of the graphThe transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = abx−h k y = a b x h k Find a a, h h, and k k for f (x) = 2x f ( x) = 2 x a = 1 a = 1 h = 0 h = 0 k = 0 k = 0 The horizontal shift depends on the value of h h



How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic
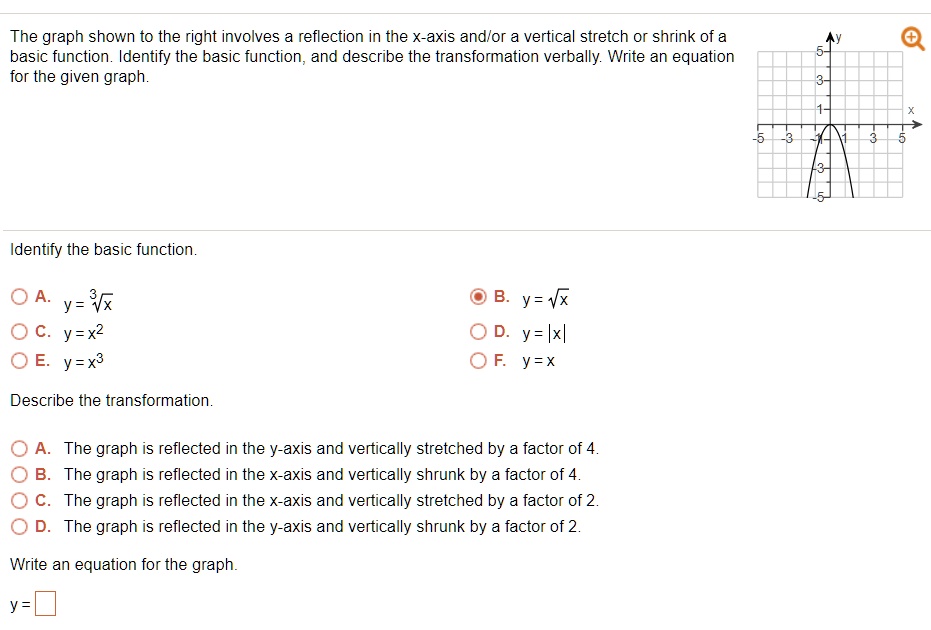



Solved The Graph Shown To The Right Involves A Reflection In The X Axis Andlor A Vertical Stretch Or Shrink Of A Basic Function Identify The Basic Function And Describe The Transformation Verbally Write
You can sketch the graph at each step to help you visualise the whole transformation eg for f (x) = x^2 4 f (x) = x2 − 4 and y=2f (x2) y = 2f (x 2), draw the graph of y=f (x2) y = f (x 2) first, and then use this graph to draw the graph of y=2f (x2) y = 2f (x 2) Note These transformations can also be combined with modulus functionsGraph the Function Using Transformations Examples 5 is added to the function, so we have to move the graph of y = 3(x1) 2, 5 units to the left side Apart from the stuff given above, if you need any other stuff in math, please use our google custom search hereNote When using the mapping rule to graph functions using transformations you should be able to graph the parent function and list the "main" points Example 3 Use transformations to graph the following functions a) h(x) = −3 (x 5)2 – 4 b) g(x) = 2 cos (−x 90°) 8 Solutions a) The parent function is f(x) = x2



Transformations Of Y X 2 Using Desmos Teaching Resources




Applying T X Y X Y 3 On The Graph Of Y X 2 Download Scientific Diagram



Transformations Left Or Right




Ex Determine The Equation Of A Transformation Of Y 2 X Youtube
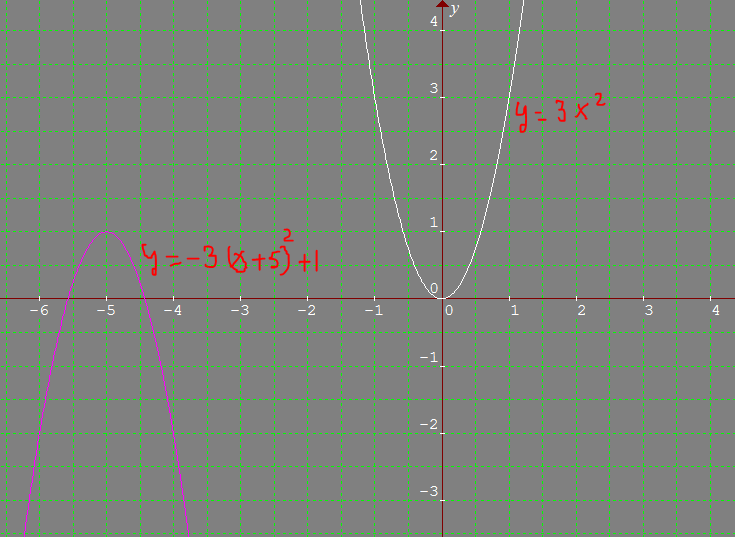



How Do You Sketch The Graph Of Y 3 X 5 2 1 And Describe The Transformation Socratic
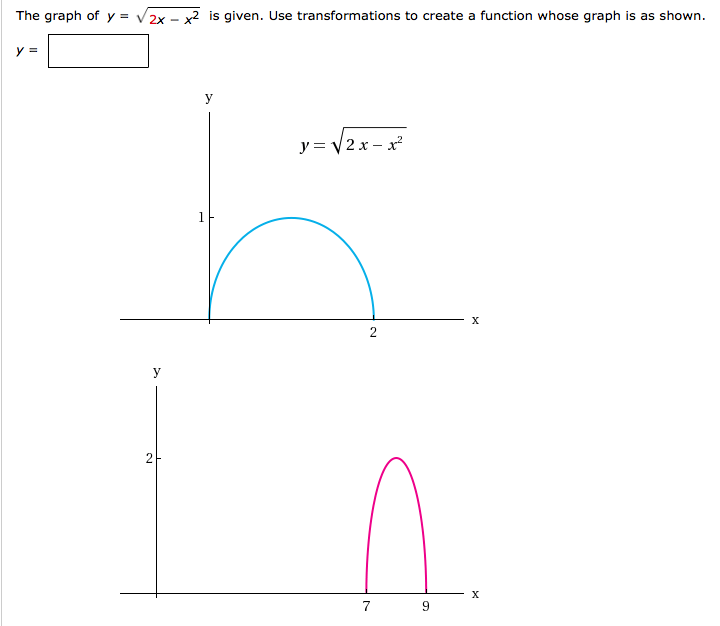



Solved The Graph Of Y Square Root 2x X 2 Is Given Use Chegg Com
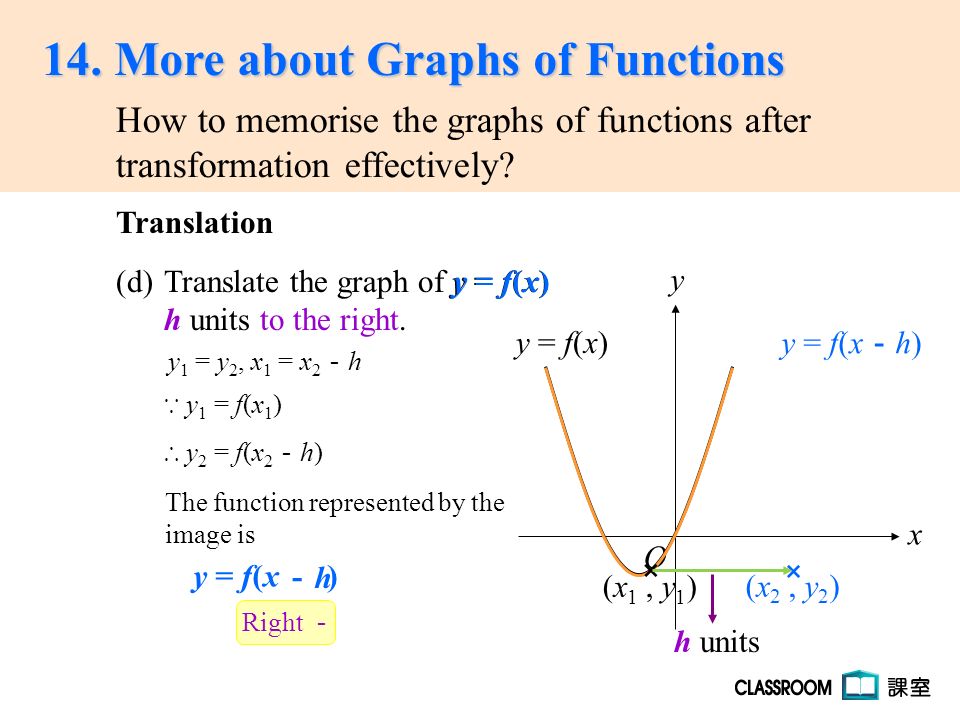



14 More About Graphs Of Functions Transformation Effectively How To Memorise The Graphs Of Functions After O Y X A Translate The Graph Of Y F X K Ppt Download
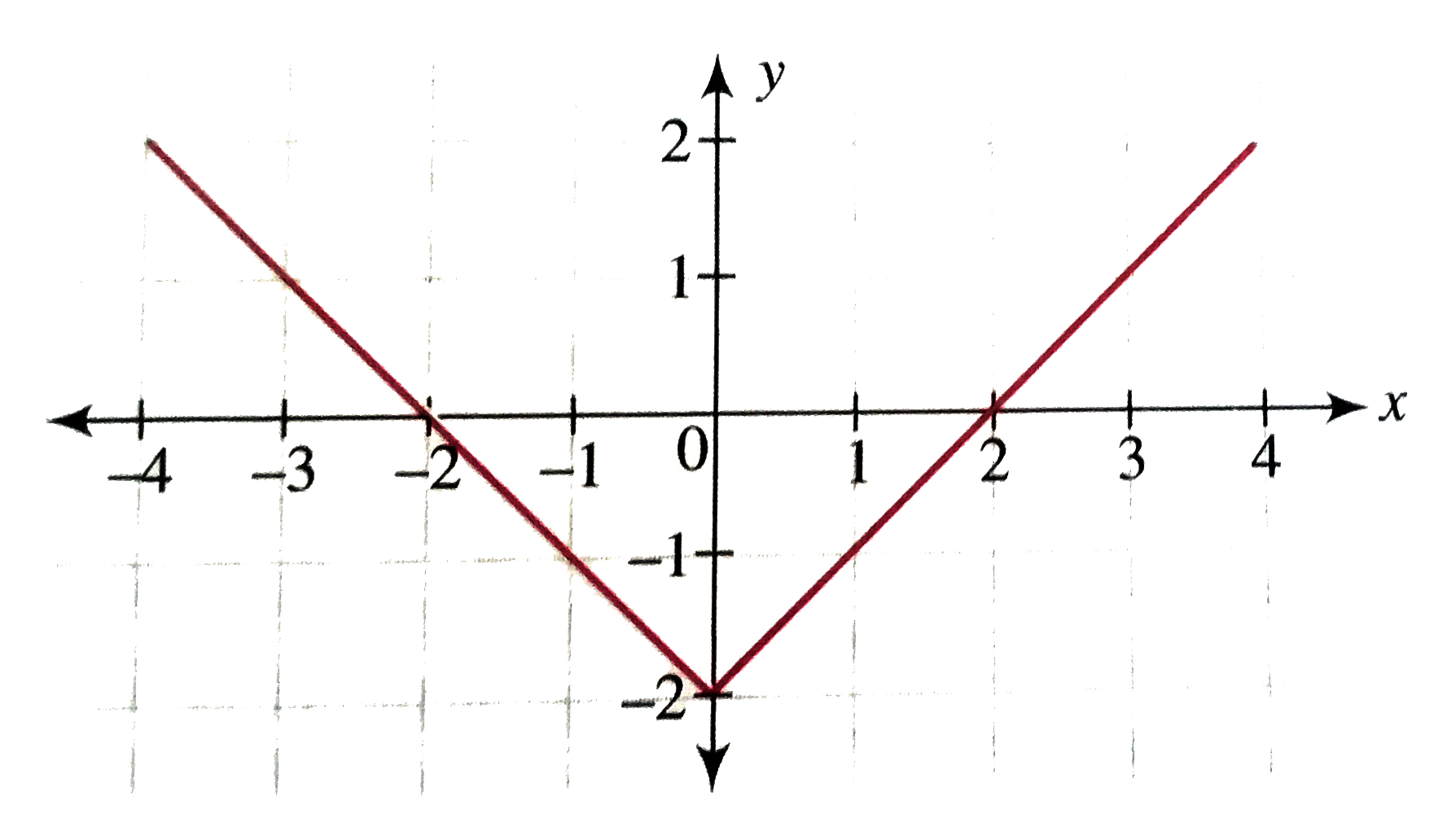



Draw The Graph Of X Y 2 Using Graphical Transformation



2



Solution Graph The Function F By Starting With The Graph Of Y X2 And Using Transformations Shifting Compressing Stretching And Or Reflection Hint If Necessary Write F In The




The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com
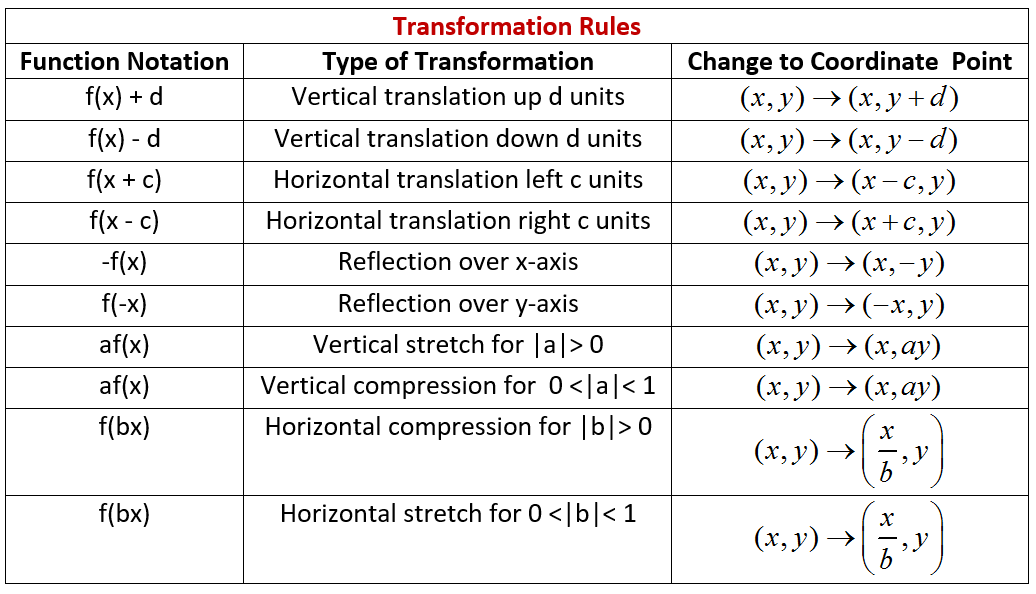



How Do You Sketch The Graph Of Y X 2 2 2 And Describe The Transformation Socratic
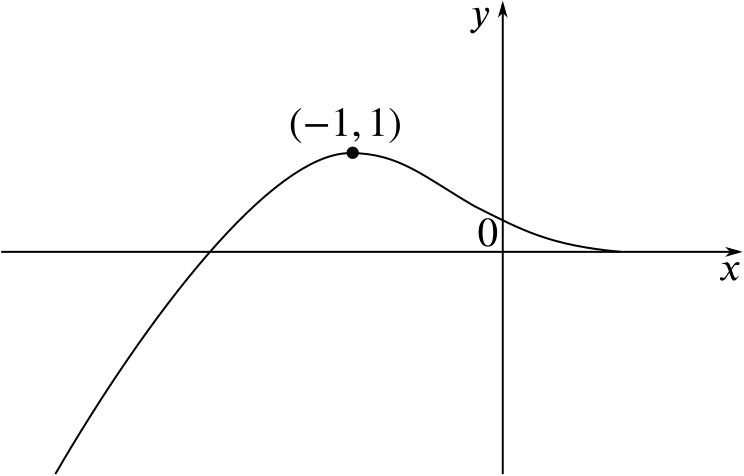



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics
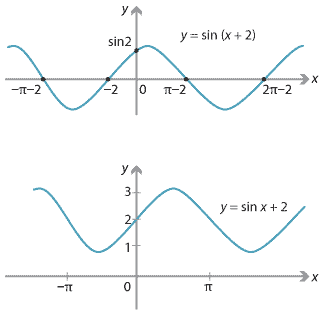



Content Geometric Transformations Of Graphs Of Functions




Begin With The Graph Of Y Ln X And Use Transformations To Sketch The Graph Of




Content Transformations Of The Parabola




Transformations Of Graphs




Graph The Function By Hand Not By Plotting Points But By Starting With The Gra




Graphing Shifted Functions Video Khan Academy




Symmetry Transformations And Compositions




1 07 Transformations Of Functions
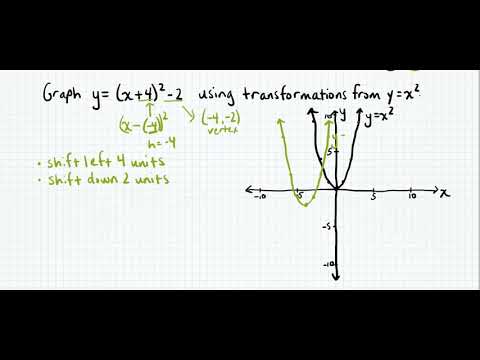



Graphing Transformations Of Y X 2 Youtube




Transforming Exponential Graphs Example 2 Video Khan Academy




Transformations Of Quadratic Functions College Algebra




Transformations Of Y X Ck 12 Foundation




Using Transformations To Graph Functions



Jdlogo Home Functions Defined Functions You Should Know Transformations Of Quadratics Translations Reflections Inverses Stretches Combinations Combining Functions Review Test Unit 2 Functions And Transformations Lesson 3a
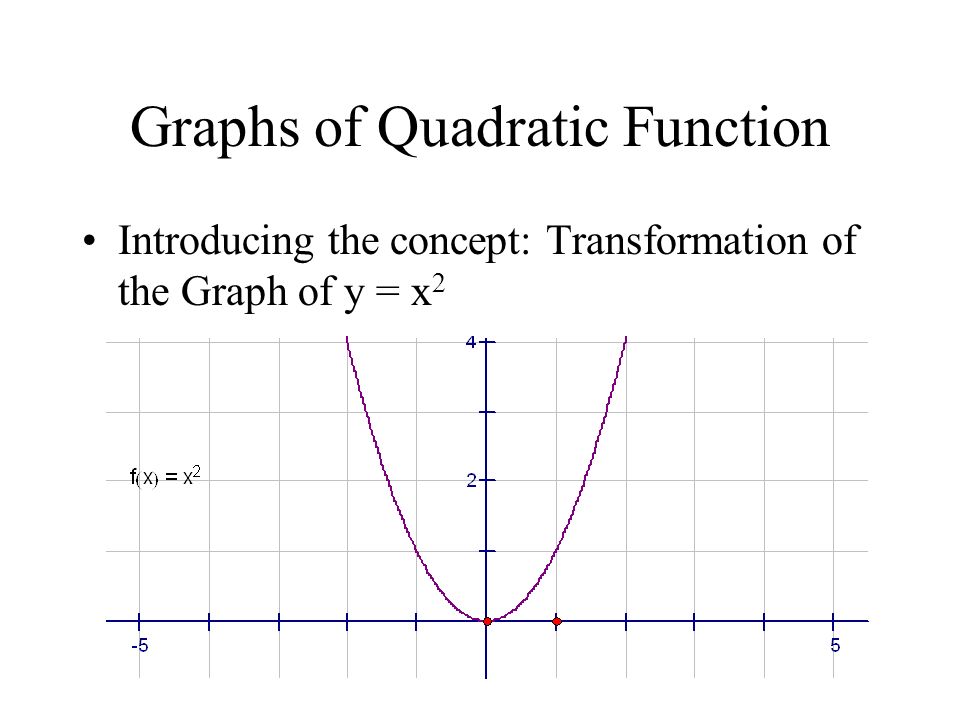



Graphs Of Quadratic Function Introducing The Concept Transformation Of The Graph Of Y X Ppt Download



Transformations Of Functions Mathbitsnotebook A1 Ccss Math



What Transformations Are Needed To Transform The Graph Of The Parabola Y X 2 Into The Graph Of The Parabola Y X 2 4x 6 Quora



1
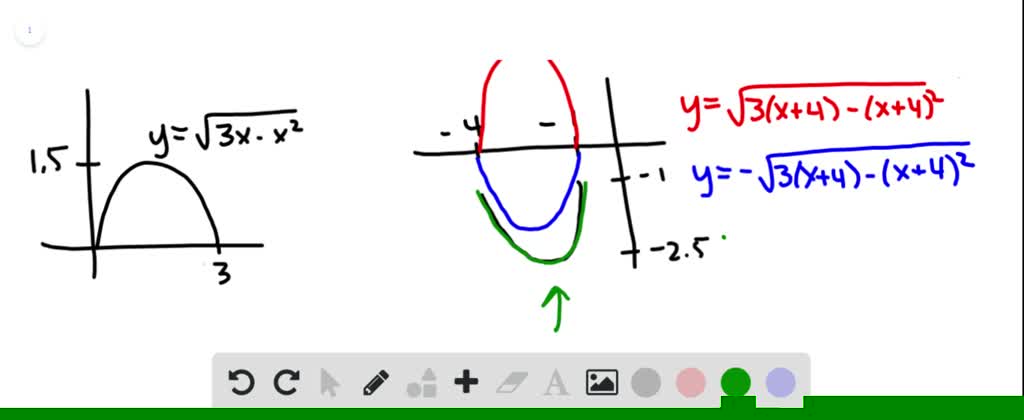



Solved The Graph Of Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown
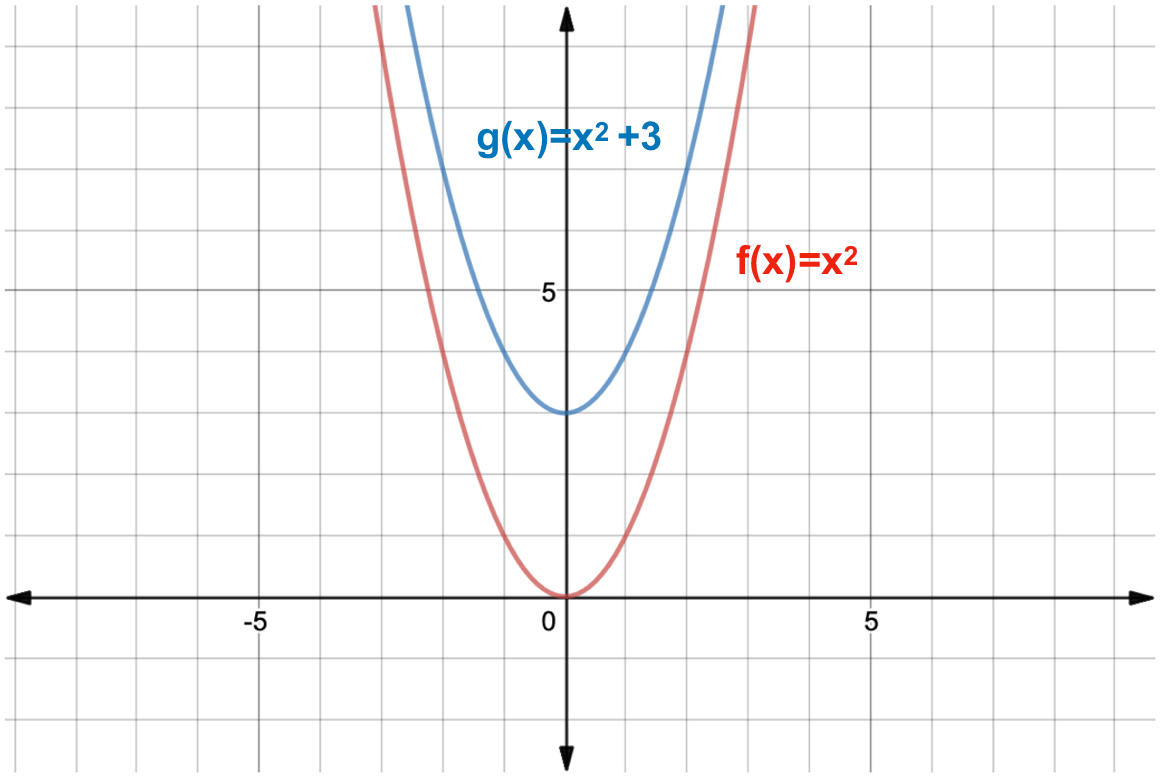



What Is A Function Transformation Expii
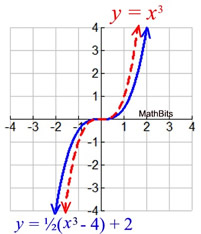



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math
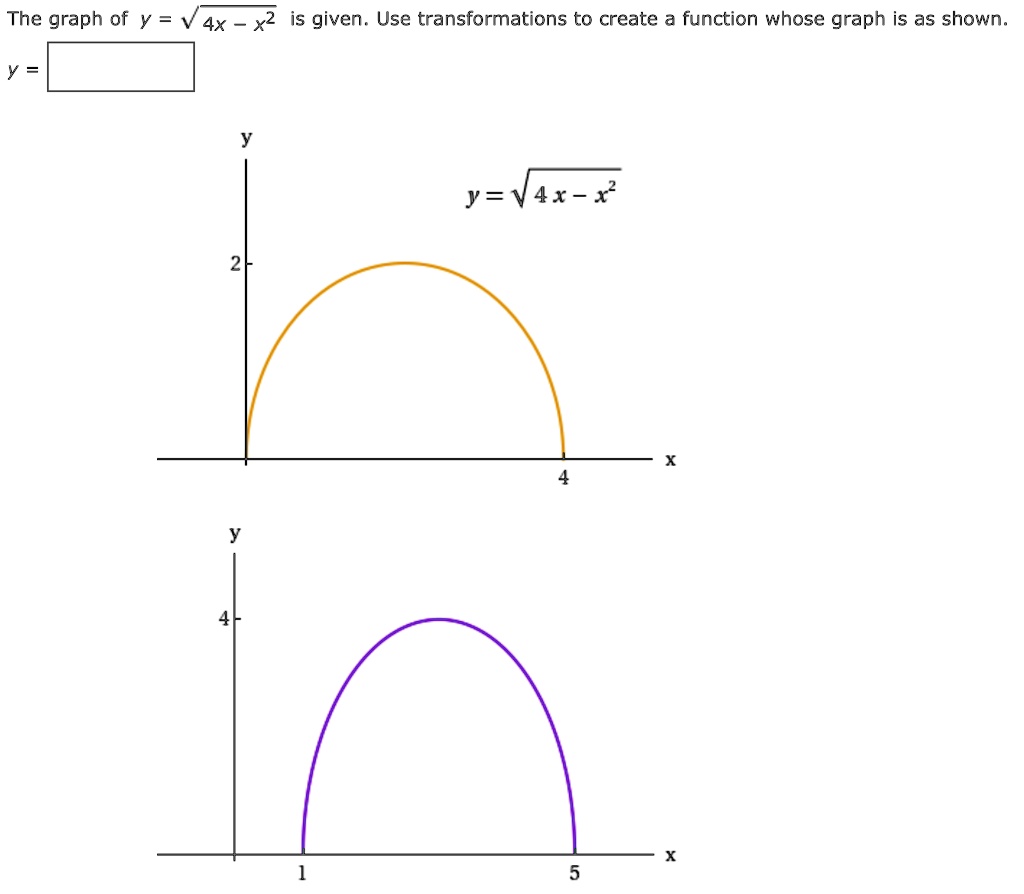



Solved The Graph Of Y 4x X2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Y V4x X



Discovering Advanced Algebra Resources




Solved Write The Equation Of A Function That Is Finally Graphed After The Following Transformations Have Been Applied To The Graph Of Y X 1 Reflected Over The X Axis 2 Shifted Right Units 0
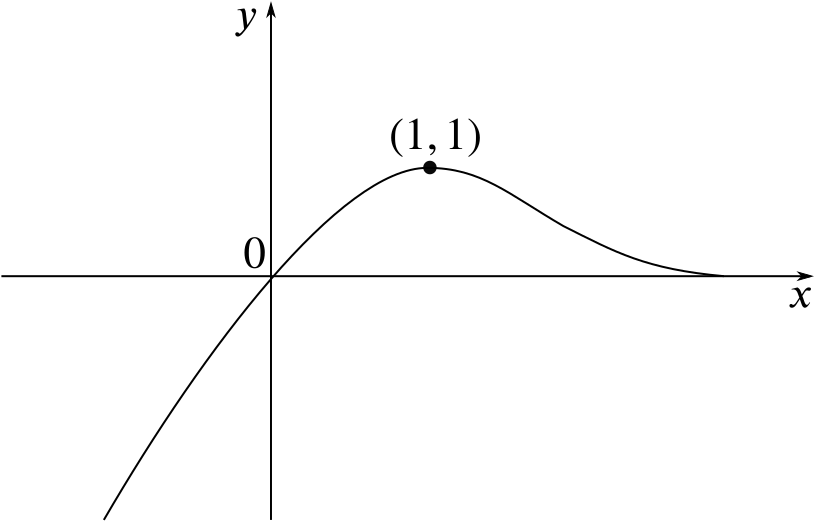



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics
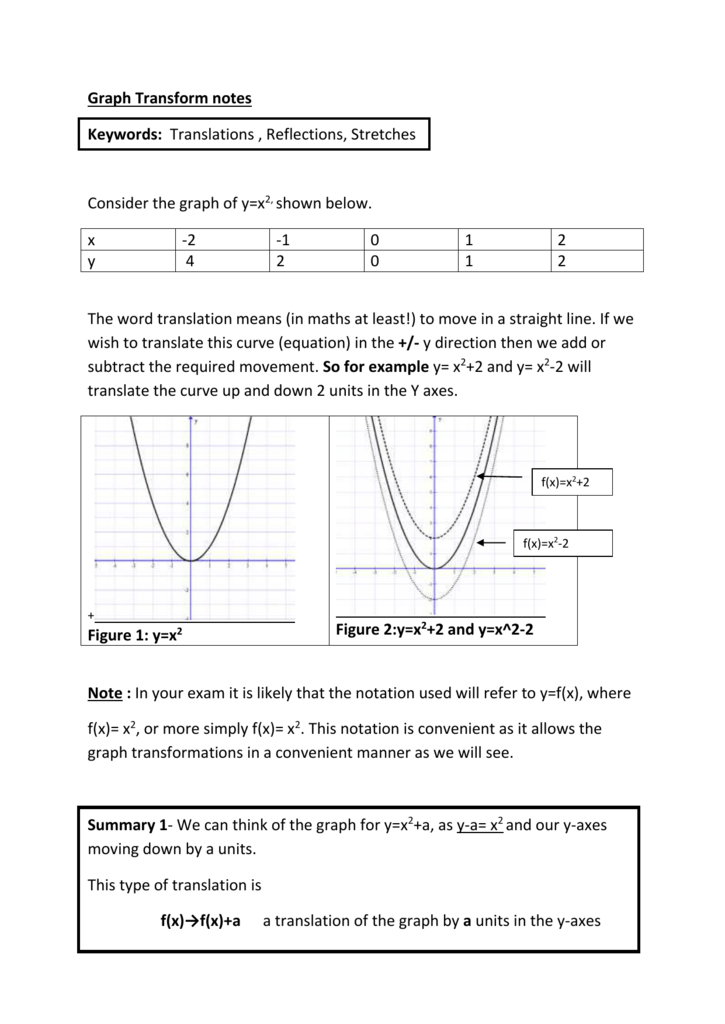



Graph Transform Notes
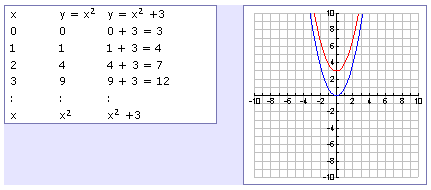



Transformations



Biomath Transformation Of Graphs



Describe The Geometrical Transformation That Maps The Graph Of Y X 2 Onto The Graph Of Y X 2 2x 5 Enotes Com
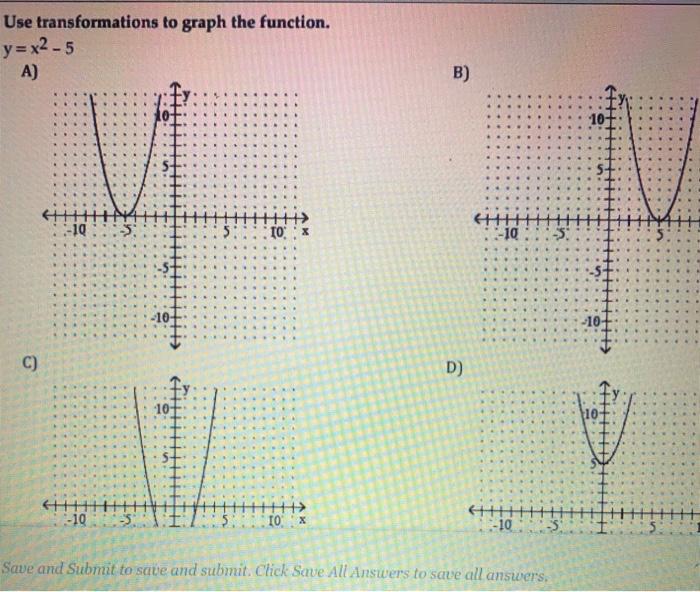



Solved Use Transformations To Graph The Function Y X2 5 A Chegg Com



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




Describe The Transformations Of The Graph Of Y X That Will Produce The Graph Of Y X 2 2 3 Brainly Com
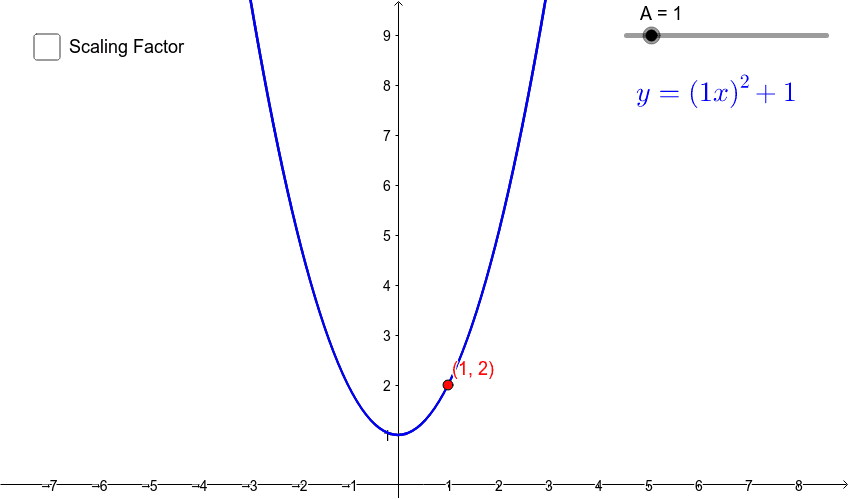



Stretch Parallel To The X Axis Geogebra



Solution I Have A Question That States A Use The Transformations On The Graph Of Y X 2 To Determine The Graph Of Y X 5 2 9 B Using The Graph Of F X X 2 As A Guide Graph
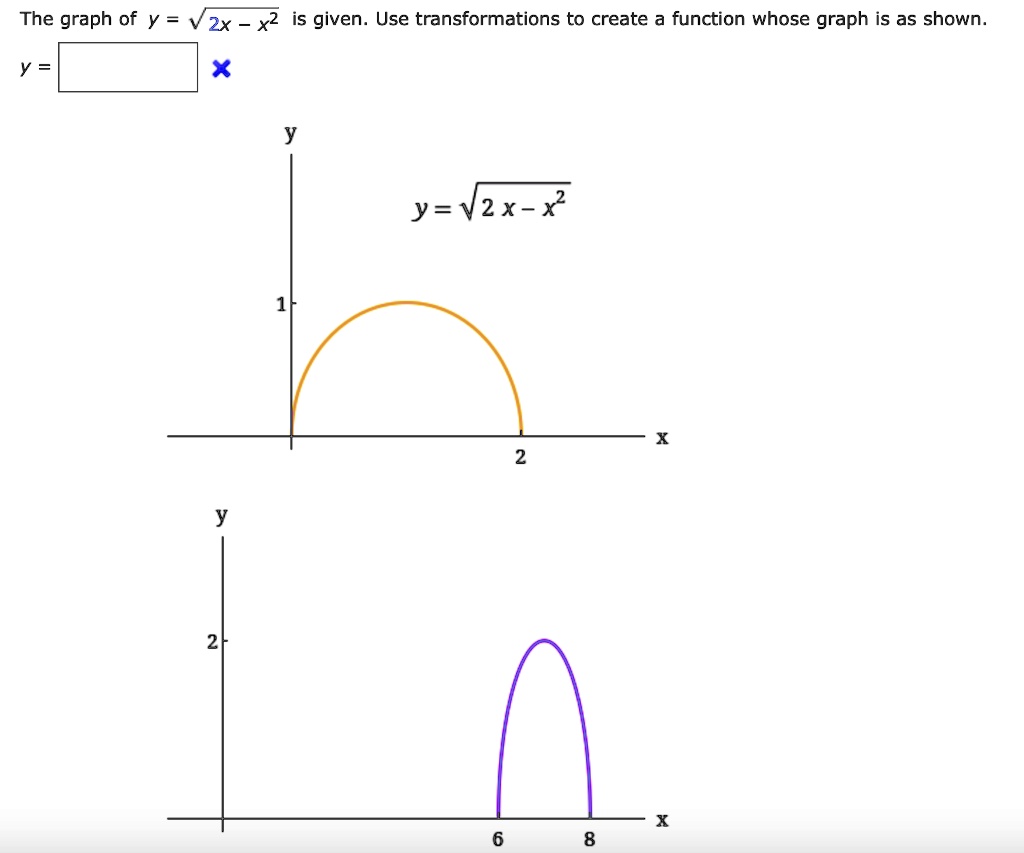



Solved The Graph Of Y 2x X2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Y Vzx X




Graph Transformations With Examples Gcse Mitch Maths
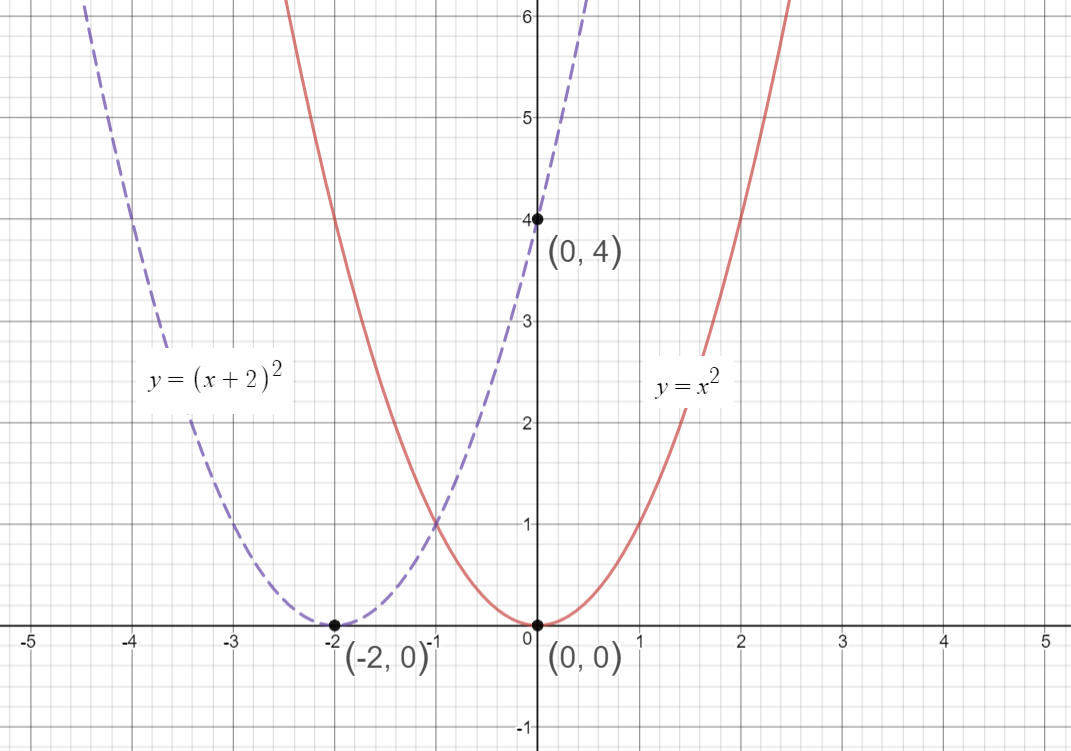



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic
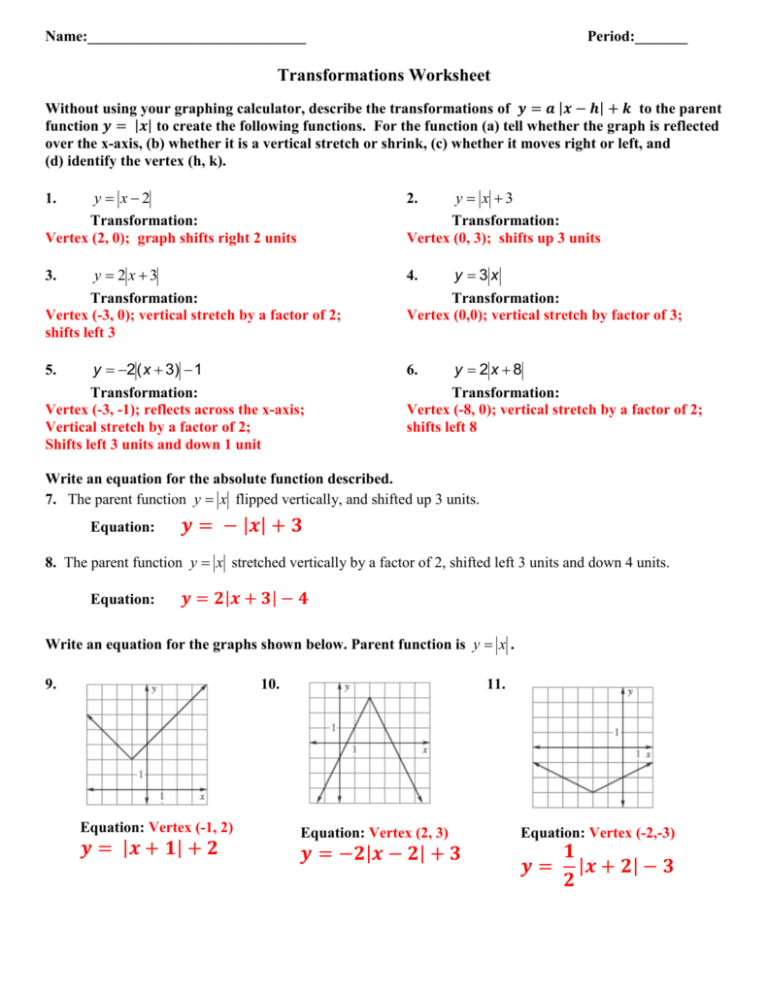



Absolute Value Transformations
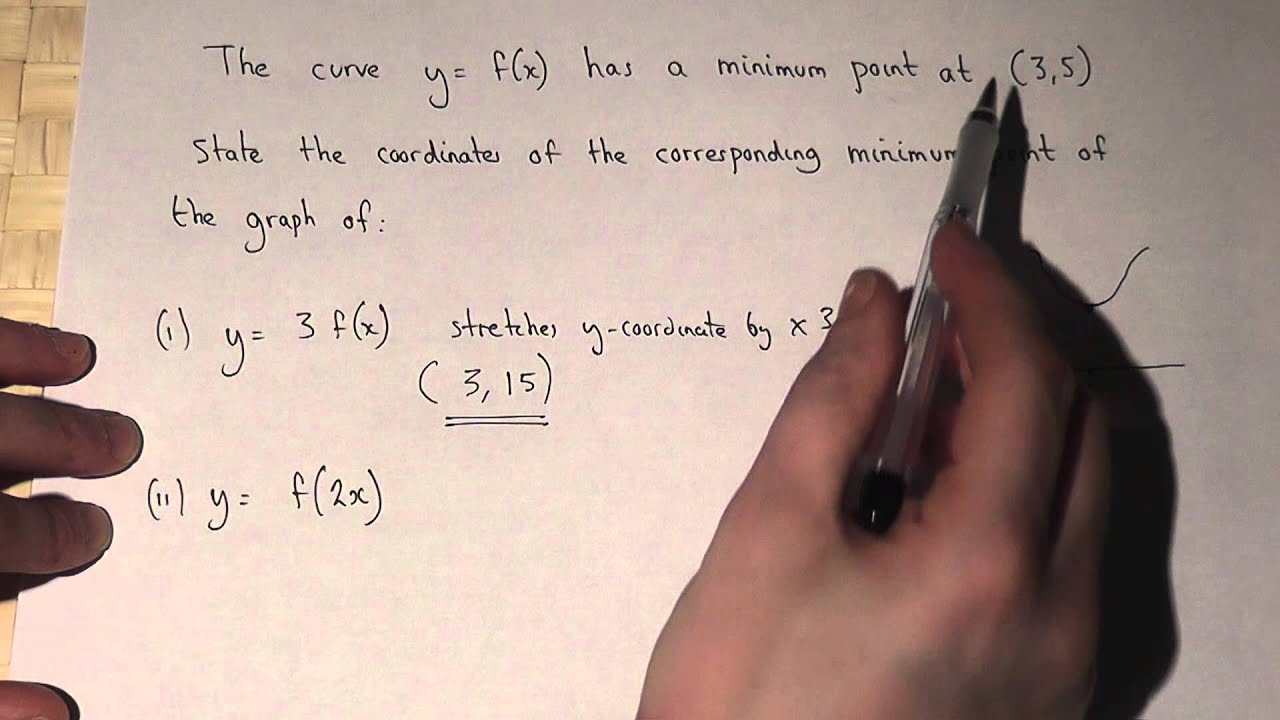



Graph Transformations Y 3f X And Y F 2x Youtube




Transformations Of The 1 X Function Video Lesson Transcript Study Com




Transforming Graphs Of Functions Brilliant Math Science Wiki




Solved Graph The Function F By Starting With The Graph Of Chegg Com




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
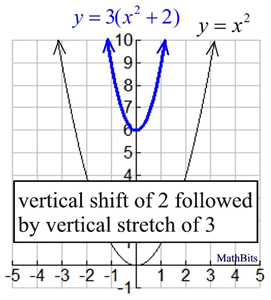



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic



Transformations Of Functions




Solved Use Transformations Of The Graph Ofy X5 To Graph The Function H X 2 X 3 5 Which Transformations Are Needed T0 Graph The Function H X 2 X 3 52 Choose The Correct
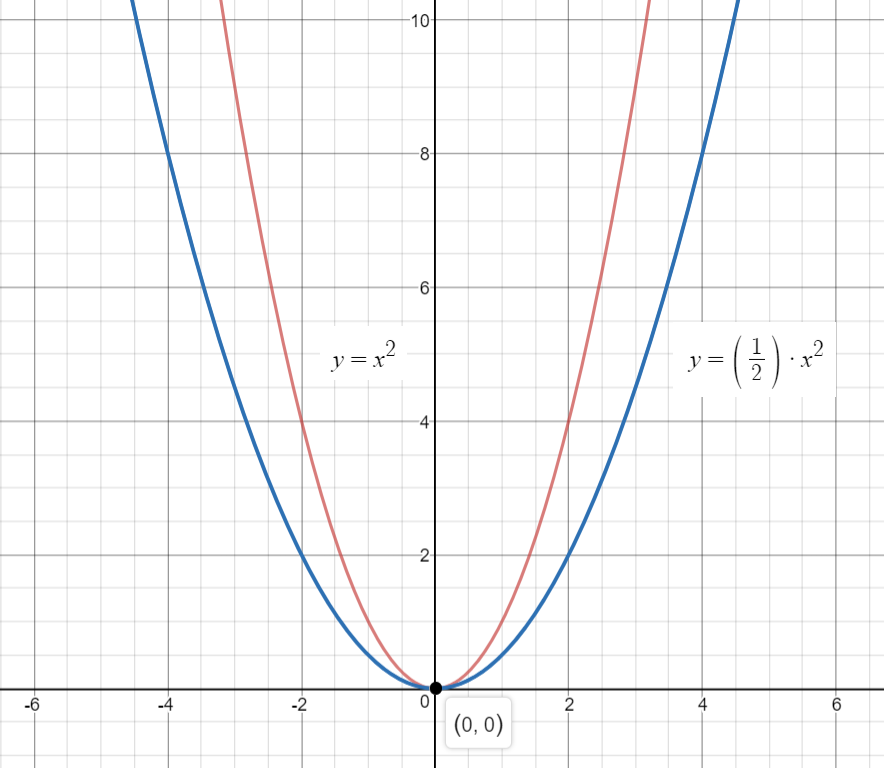



How Do You Sketch The Graph Of Y 1 2x 2 And Describe The Transformation Socratic




Transformations Past Edexcel Exam Questions
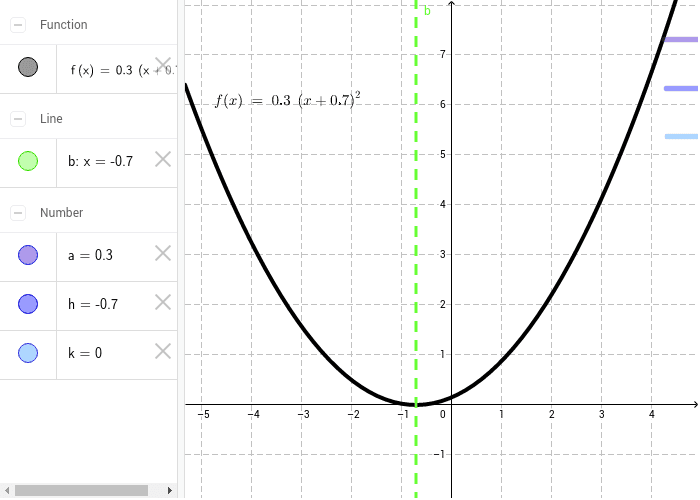



Transformations To The Graph Of Y X 2 Geogebra
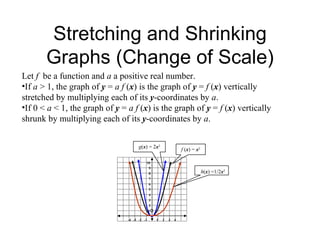



Transformations




Graphing Functions Interpret The Graph Of Frac Ax B Cx D As A Transformation Of Y Frac 1 X Mathematics Stack Exchange
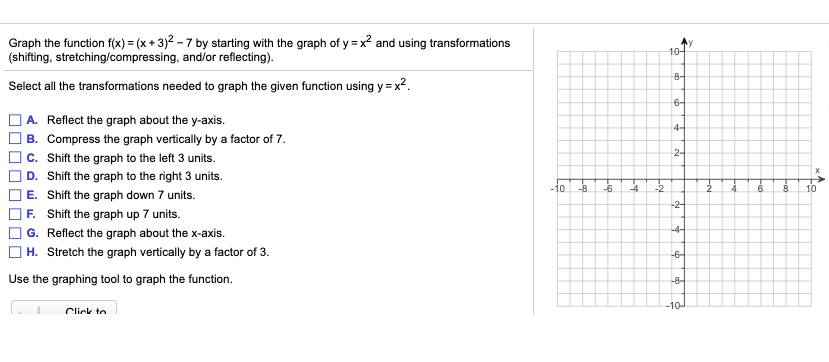



Solved Graph The Function F X X 3 2 7 By Starting With Chegg Com



Exploring Transformations Of Parent Functions
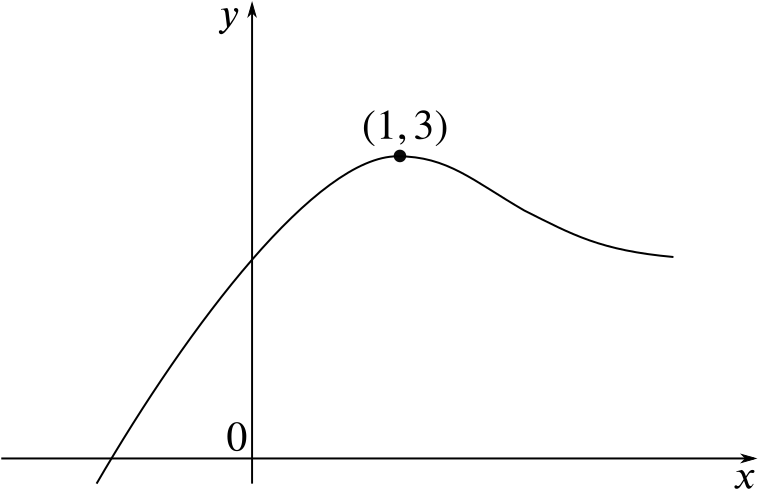



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics



How Would The Graph Of Math Y X 2 4 Math Differ From The Base Graph Of Math Y X Math Quora



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



Parabola Parent Function Mathbitsnotebook Ccss Math




The Transformation Of The Graph Of A Quadratic Equation Matherudition




How To Graph Transformations Of Functions 14 Steps



3 What Transformations Must Be Applied To The Grap Gauthmath
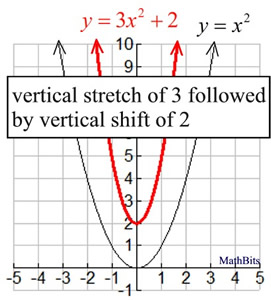



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math




Content Transformations Of The Parabola




Transformations Of Functions Ck 12 Foundation
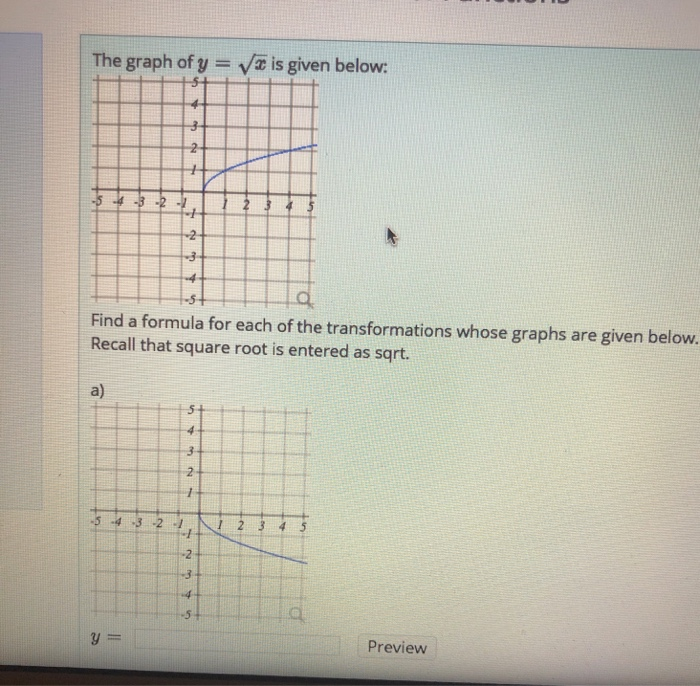



Solved The Graph Of Y X Is Given Below 3 Ch No 2 3 4 5 Chegg Com



0 件のコメント:
コメントを投稿